立方体と直方体って何が違う? 立方体の体積問題を解説! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?このプリントでは, 体積に関する性質を用いて行列式の変形を説明する 別途講義で, 以下の 性質を改めて行列式の定義式から示す 立体の体積は a b c = 1 0 0 0 2 0 0 0 2 = 4 に等しい 注意もしa, b, c の中に同じベクトルがあると, 立体がつぶれて, 体積はゼロに2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい

スタディピア 立体の体積
台形 立体 体積 公式
台形 立体 体積 公式- この公式でどんなボールの体積も計算できちゃうんだ。 たとえば、半径30 cmのサッカーボールがあったとしよう。 こいつの体積は「4/3 × π × 半径の三乗」という公式をつかってやると、 ³ 4 3 × π × 30 × 30 × 30 = π c m ³ 単元 立体の体積と表面積, 「角柱、円柱、円錐、球、の体積と表面積の公式がややこしくてワケわからなかったので、頭を整理するために1ページにまとめてみました。定期テストが始まるまでトイレに貼っておくために作りました😅」, 学年 中学1年生, キーワード 空間図形,立体,体積,表面積




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ
切頭三角柱の体積を求める公式 前回 に引き続き、斜めに切断された立体(切頭〇〇柱)の体積を求めるテクニックを紹介します。 今回は切頭三角柱です。 早速例題を見てみましょう。 この問題を普通に解こうとすると、かなり手間がかかります体積 ③ 5年 組 名 前 (教科書〜23ページ) 右のような立体の体 たいせき 積の求 もと め方を 考えましょう。 組み合わせた立体の体積 容積と体積の単位 1L の水を,内のりがたて10cm,横10cm の 容 よう 器 き に入れると,高さが10cm になります。47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。
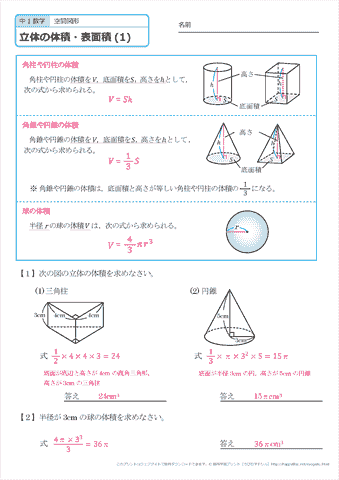
柱の体積 = 底面積 × 高さ1 右図の四角柱の体積は (cm 3) 底面積は S=3×4=12 (cm2),高さは h=5 (cm)だから,体積は V=Sh=12×5=60 (cm3) 2 右図の円柱の体積は (cm 3) 底面積は S=π×3 2 =9π (cm2),高さは h=8 (cm)だから,体積は V=Sh=72π (cm3)四角錐台の体積 110 /191件 表示件数 5 10 30 50 100 0 1 01 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 建築設計の折り上げ天井の空調気積と平均天井高さ ご意見・ご感想 計算式も提示頂いてるので、根拠を示せるので助かりました。
②角柱や円柱の体積の求め方 ③角柱や円柱の体積の公式 ④生活場面での立体の体積を求めるよさ 教え方1 教え方1 5年生で勉強した直方体や立方体の体積の求める公式を生かして、四角柱の体積の求め方を気づかせます。 正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。任意の4つの頂点の座標が与えられた四面体の体積の求め方について解説します. 今までのあらゆる知識を動員して解くので演習効果が高く,個人的には,ベクトルを学ぶ目的の一つにこれを掲げてもいいのではと思っています. 目次 1: 頂点の座標が
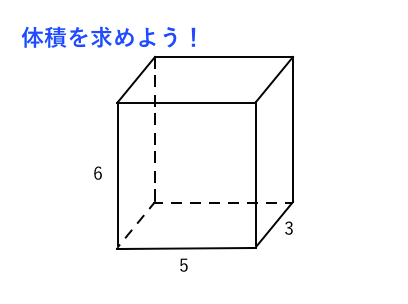



超簡単 体積の求め方 苦手な数学を簡単に
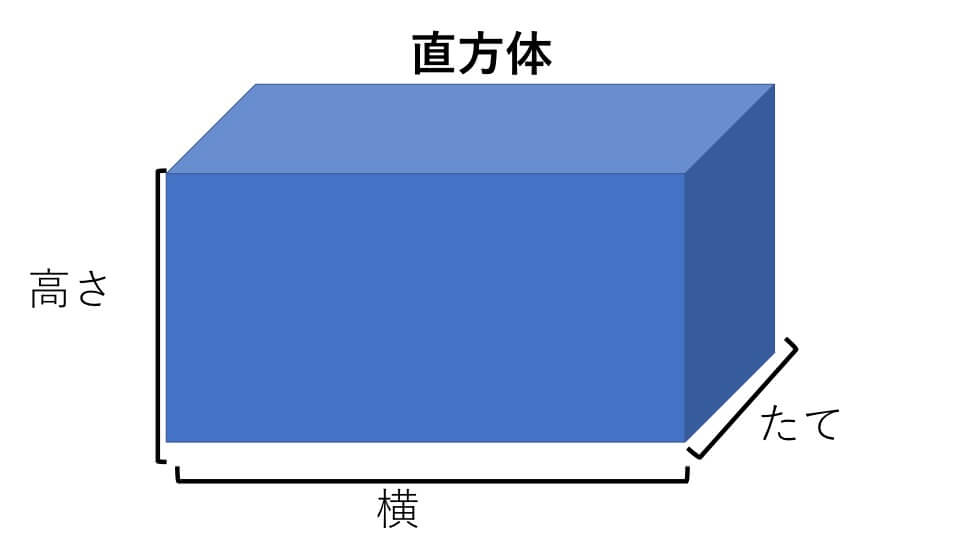



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
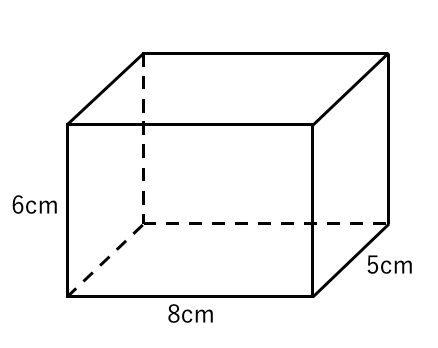
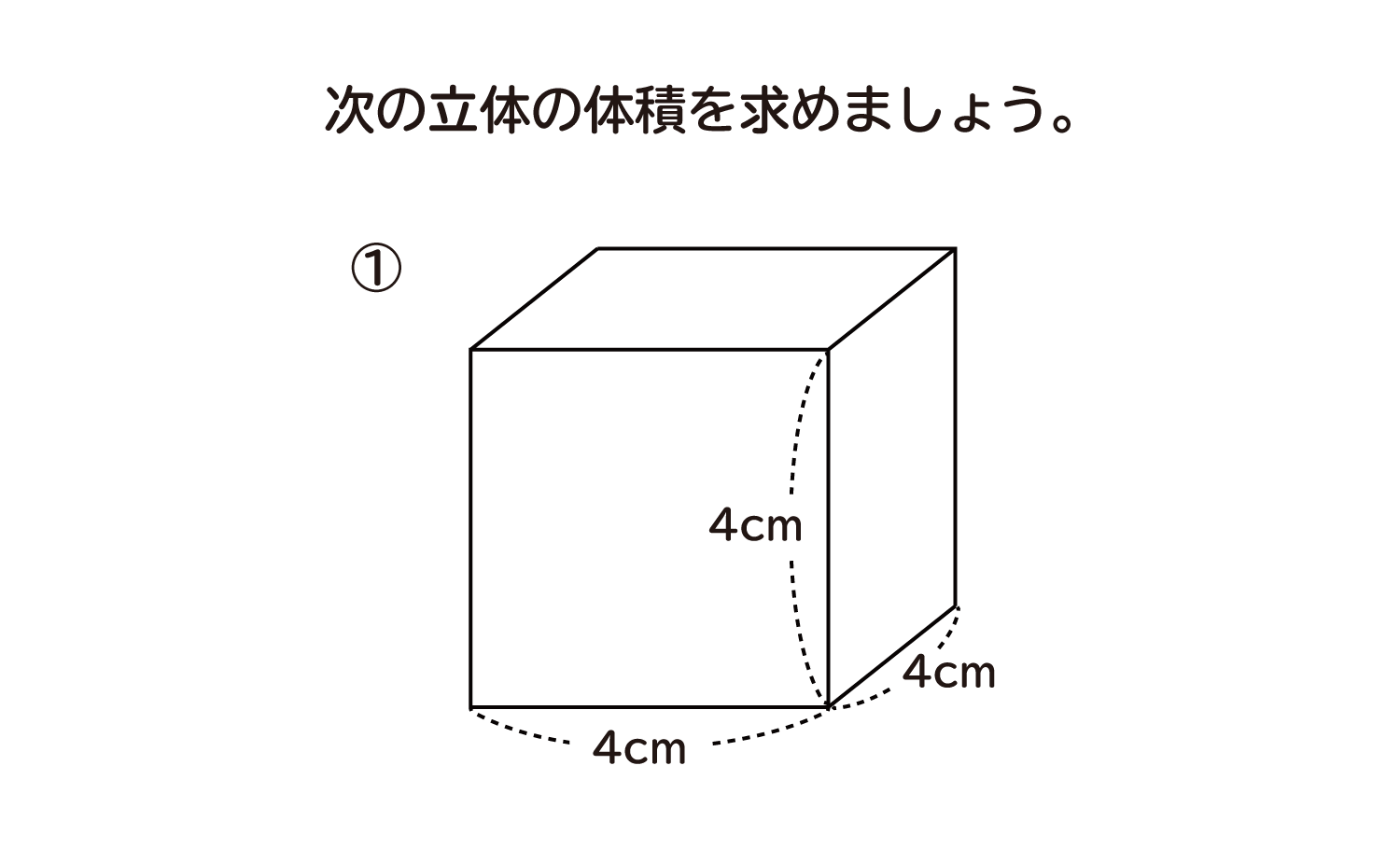
立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 (c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 (c m 3)θ d θ = 2 R 2 ∫ − π 2 π 2 1 cos 2 θ 2 d θ = 2 R 2 θ 2 1 4 sin 2 θ − π 2 π 2 = π R 2 ⋅ ⋅ ⋅ ( 8) となります。 よって、公式通りになります。 複雑な関数や3次元の体積を求める方法の基本的な積分はこのような手法であると思います。 しかし、何も体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。




体積の求め方 公式一覧 小学生 中学生の勉強




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス
た立体と考えることができます(数学の世界では,円 えん 環 かん 体 たい またはトーラスと呼ばれています)。 円の重心はその中心と一致するので,もとの円の半径と,円の中心と直線との距離がわかれば,ドーナツ形 の体積を求めることができます。体積 = 半径 × 半径 × 314 × 高さ立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し, x における断面積を S (x) とおきます. 上で復習した面積の求め方と同様にして ⊿V (x)≒S (x)⊿x




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の体積ってなんであの公式なの Webty Staff Blog
この公式を使う例題・証明・および回転体の体積を求める他の公式を紹介します。 (ただし 0 ≤ α < β 0\leq \alpha付録 (公式集) 土塁,土橋,堀などの体積計算に有用であった公式を挙げる.その証明 西村 06 も示す. 公式 1 四角錐台の体積 上下の底面が長方形で,対応する各辺(縦 a と c;横 b と d )が並行であり, 高さ h の四角錐台 (稜線は 1 点で交わらなくてもよい) (付図 1) の体積:
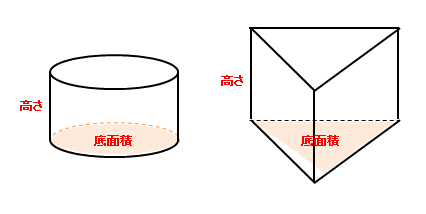



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin立体の体積&容積および諸数値 V=容積、S=表面積、As=側面積、Ab=底面積、x=底面より重心までの距離 寸 法 容積および諸数値 寸 法 容積および諸数値 V=a 2 S=6a 2 As=4d 2 正多角形 a=辺長公式計算 平面図形の面積(a),周長(l)および重心位置(g) p11 平面図形の性質 p12 立体の体積(v),表面積(s)または側面積(f)および重心位置(g) p12
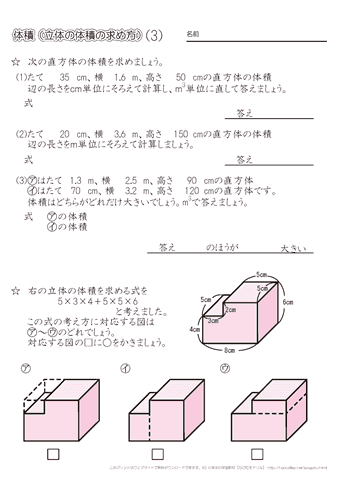



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




体積の求め方 計算公式一覧
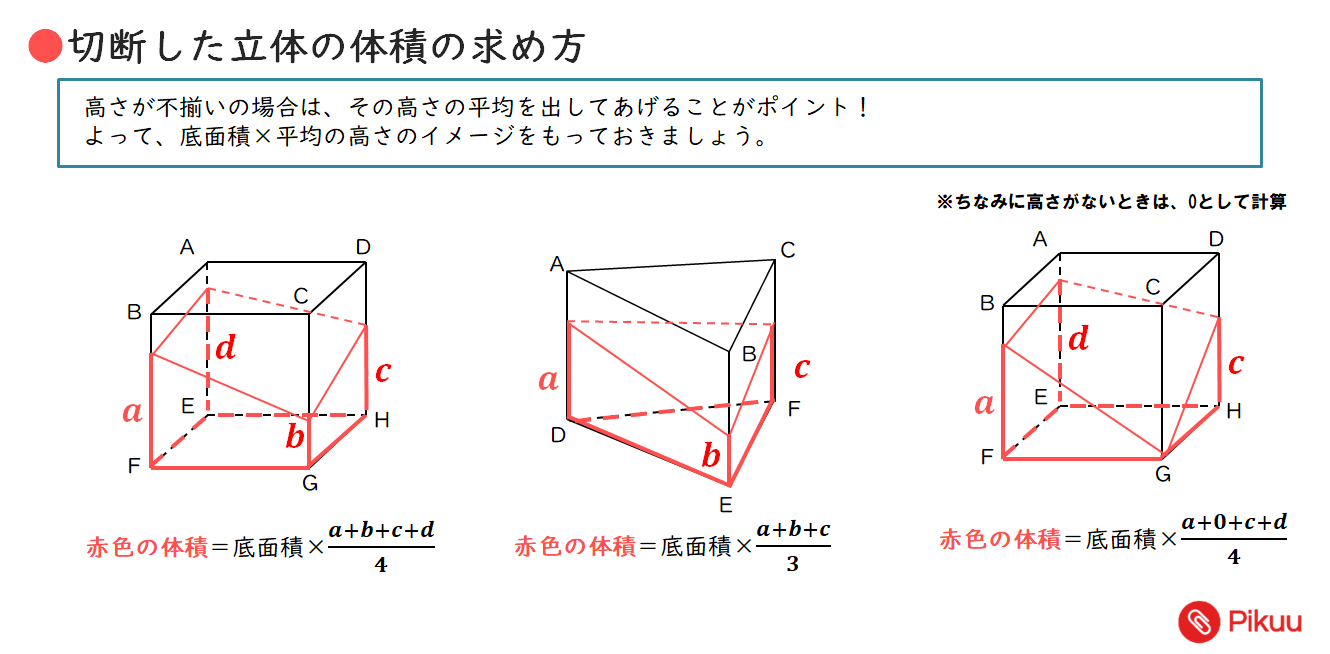
立方体の体積の求め方公式 サイコロの形をしている立方体は、一辺の長さがどれも同じ。 立方体の体積は、次の公式で求められます。 立方体の体積=1辺×1辺×1辺 直方体の体積の求め方公式 直方体の体積は、次の公式で求められます。 積分計算による体積の求め方! 断面積の積分や回転体の体積 21年2月19日 この記事では、「立体の体積を積分計算で求める方法」についてわかりやすく解説していきます。 各種公式や問題の解き方なども説明していくので、ぜひこの記事を通して 右の図は直方体を斜めに切断したものです。 この立体の体積を求めてください。 入試では非常に有名な問題で、これは次のように解くというのが「常識」のようです。 36 × 11 6 4 9 4 = 270 つまり、「高さの平均」のようなものを考えて、それを底面積




円柱の体積の求め方 公式 小学生 中学生の勉強




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく
立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答そこで、四角柱の体積=底面積×高さと見ることもできると理解させます。 ② 直方体の体積=たて×よこ×高さの公式から、図のように そして、①、②の両方から 四角柱の体積=底面積×高さ と見ることができることをまとめるのです。 柱の体積 = 底面積 × 高さ 表面積 = 底面積 × 2 側面積




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
公開日 / 最終更新日 小6算数「立体の体積」は公式が大事! 勉強方法・考え方を紹介! 立方体・直方体も角柱・円柱も体積を求めるのが苦手、という人も多いかもしれません。 しかし、実際には決まった公式に当てはめるだけで



6年算数立体の体積その2 教え方




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




円錐の体積の求め方 公式と計算例




中1数学 立体の体積 練習編 映像授業のtry It トライイット




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




小6 算数 立体の体積 小学生 算数のノート Clear




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



1



地図の体積計測




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
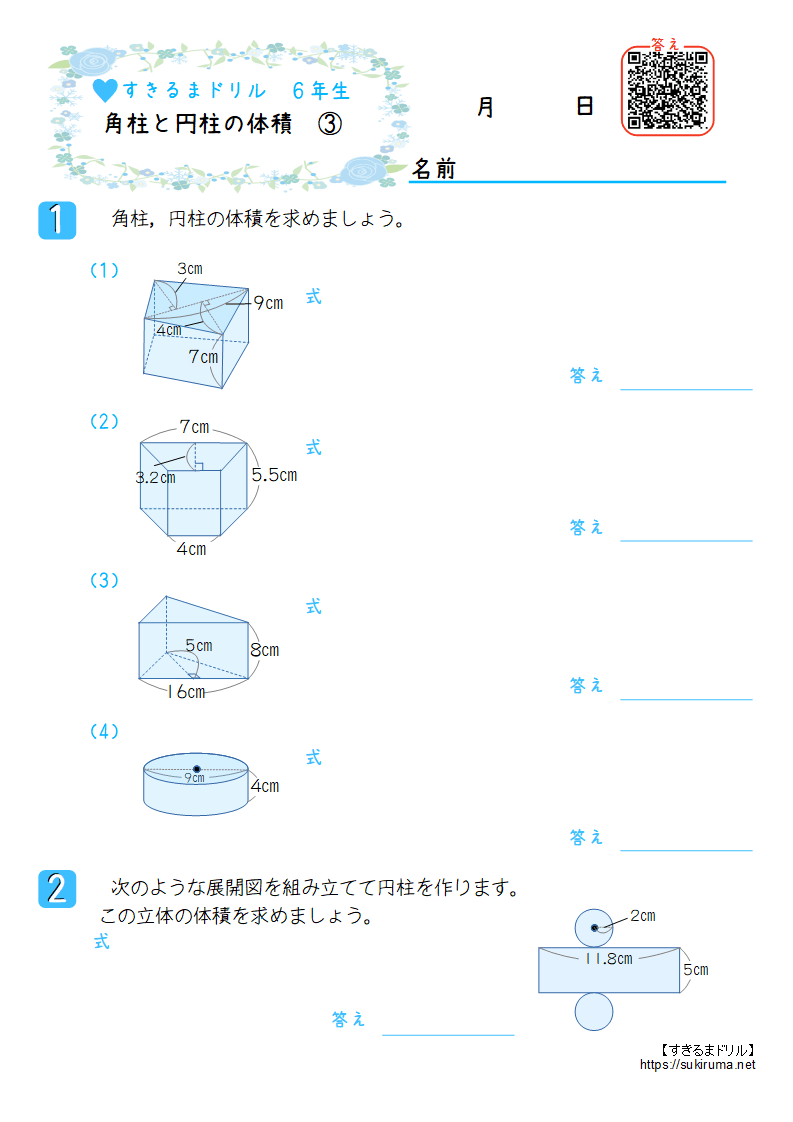



すきるまドリル 小学6年生 算数 角柱と円柱の体積 無料学習プリント すきるまドリル 無料学習プリント




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学



四角柱の体積の公式は 1分でわかる求め方 公式と計算 表面積




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




球の表面積と体積の公式 数学fun




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立体の体積を求める公式
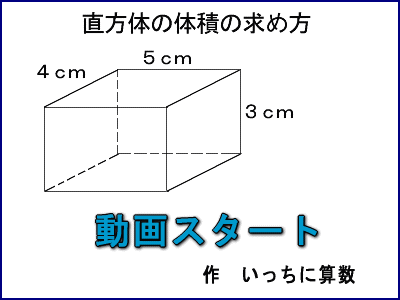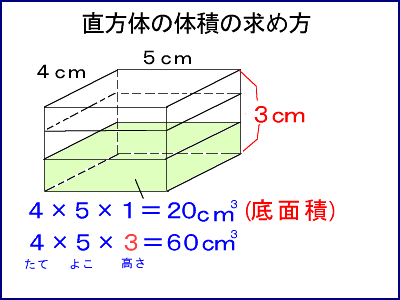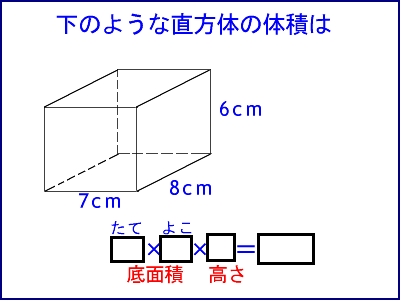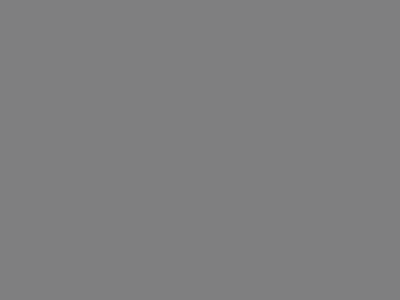



6年算数立体の体積1 教え方




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



無料 中1数学 基本解説 問題プリント 空間図形5 立体の体積 143




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト



立派な 台形 体積 求め 方




角錐 円錐の体積と表面積の公式 数学fun




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ



わかりやすく 台形の体積の求め方を教えてください わかりやすく 台形の Yahoo 知恵袋
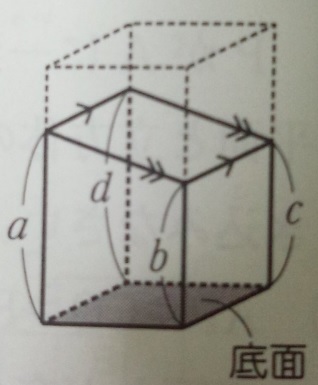



立体図形を斜めに切断した時の体積は 底面積 高さの平均 中学受験 塾なし の勉強法




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




円錐の体積ってなんであの公式なの Webty Staff Blog




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の体積を求める Youtube




中1 数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear




スタディピア 立体の体積
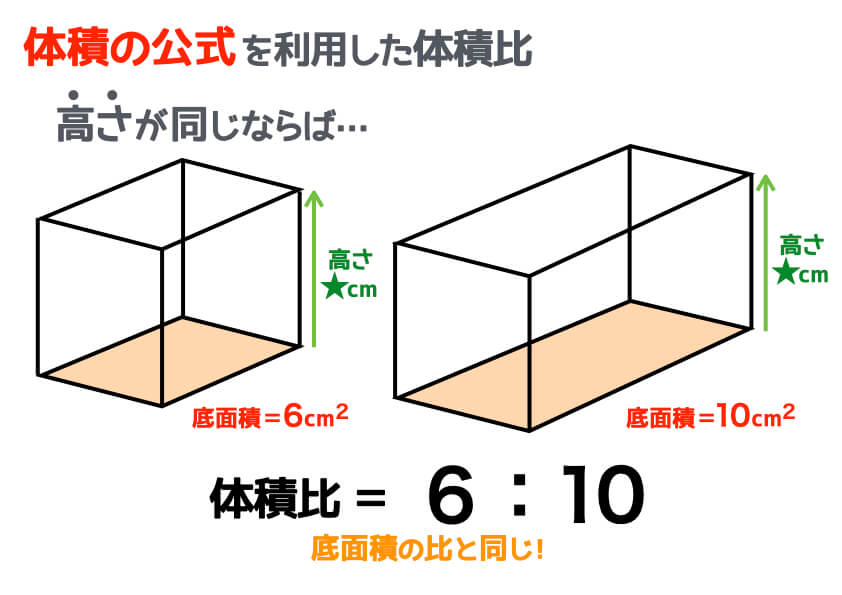



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




丸棒の重量 円柱の体積と重量の求め方 鉄の場合




どうして1 3なの 錐の体積の公式の求め方 まなべーと




体積の求め方 計算公式一覧



立体の体積を求める 苦手な数学を簡単に



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル




公式を図解 すい体の体積 円すいの表面積の求め方




体積の求め方 計算公式一覧




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




小5 算数 小5 3 直方体と立方体の体積 Youtube



高校入試対策数学 切断した立体の体積を求める練習問題 Pikuu




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



1




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



3



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル
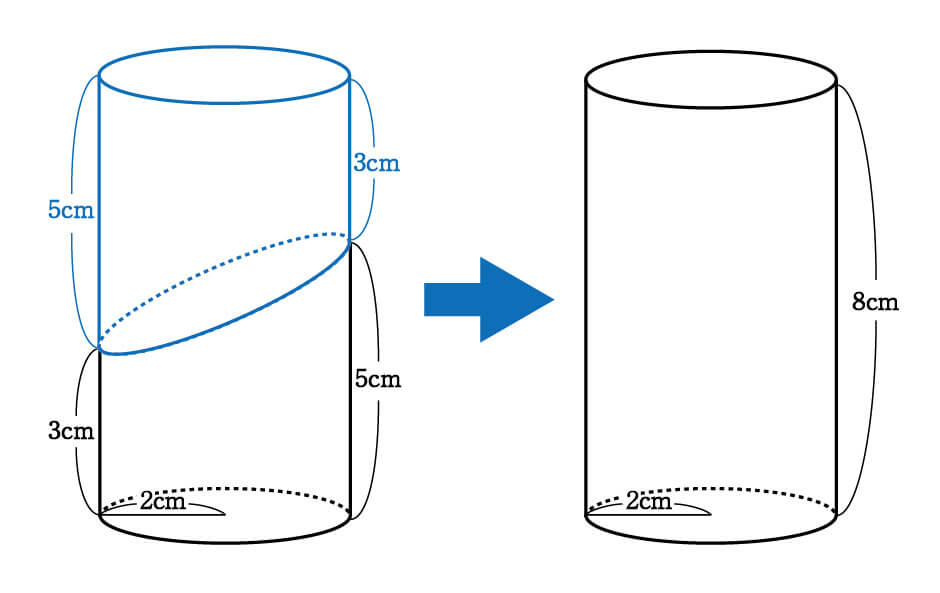



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




体積 表面積




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館
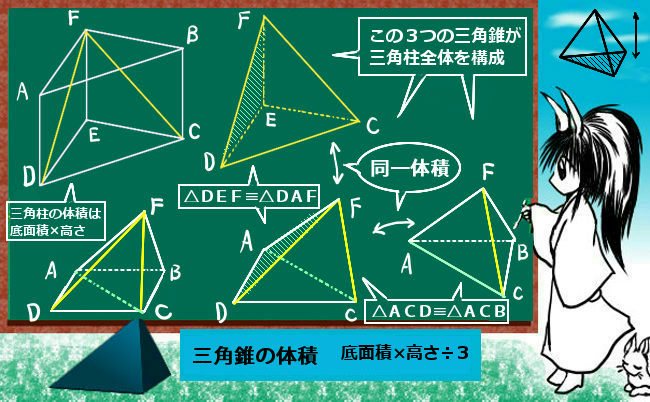



立体の体積 理数系無料オンライン学習 Kori




体積の求め方 計算公式一覧




空間図形14 円すい台の体積 Youtube




四角錐台の体積 高精度計算サイト




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




小5 算数 小5 5 体積の求め方のくふう Youtube




中1 数学 中1 立体の体積 Youtube




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学
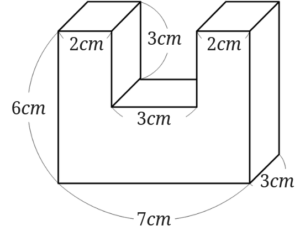



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



三角柱とは 体積 表面積の公式や求め方 計算問題 受験辞典




6年算数立体の体積1 教え方




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu



1
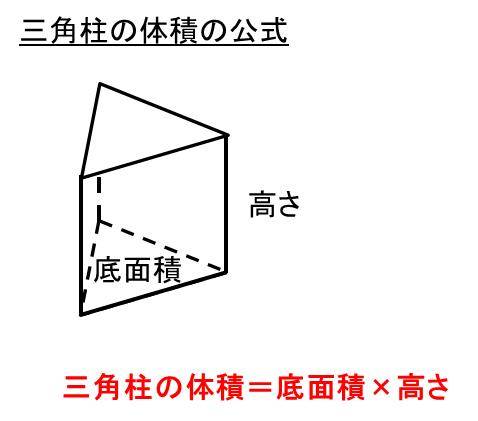



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
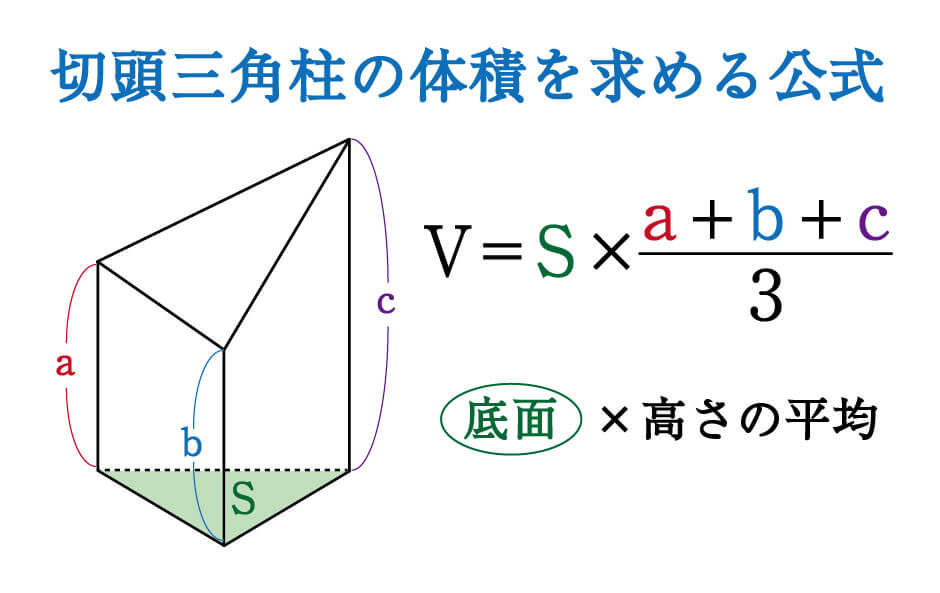



数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




小5 複雑な立体の体積 直方体 日本語版 Youtube




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成
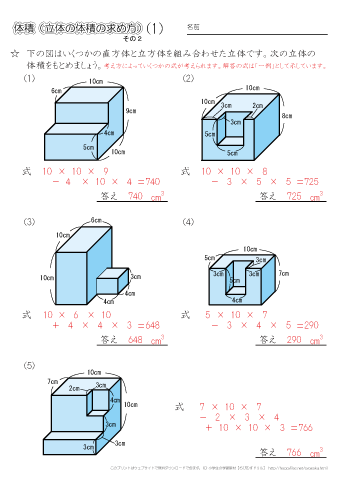



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生



0 件のコメント:
コメントを投稿