無料ダウンロード 確立 数学 171809

 数学的確率(古典的確率) 小中学校で習う確率。苦手だった人も多いはず。 統計的確率 数学的確率を少し拡張。自然と利用している事が多い気がする。 公理論的確率 現代数学における確率の考え方。統計学や人工知能の分野でよく用いられる。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 確率を求めるには、分母に"すべての場合の数"、分子に"問題にあてはまる場合の数"を入れて計算します。 まずは、"すべての場合の数"を求めていきましょう。 順番を気にする問題では 順列 Pを使う、と言いましたが、Pは紛らわしいので使わなくてもOKです（ 組み合わせ C が 大事）。 カードを1枚ずつ引いていくのを想像してください。 1枚目を引く時は

確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ

確立 数学

確立 数学-その単語が数学的な意味を持ったのは1718年からである。 18世紀に chance という単語もまた"probability"の意味で数学的に使われていた（そして確率の学説は Doctrine of Chances と呼ばれN (A)＝ 100/2 ＝50 なので、集合Aの要素の個数（2の倍数の個数）は 50個、つまり n (A)＝ 50 である。 n (B)については99÷3＝33 なので 集合Bの要素の個数（3の倍数の個数）は33個、つまり n (B)＝ 33 である。 さらに、2の倍数でもあり3の倍数でもある数の集合 A∩B

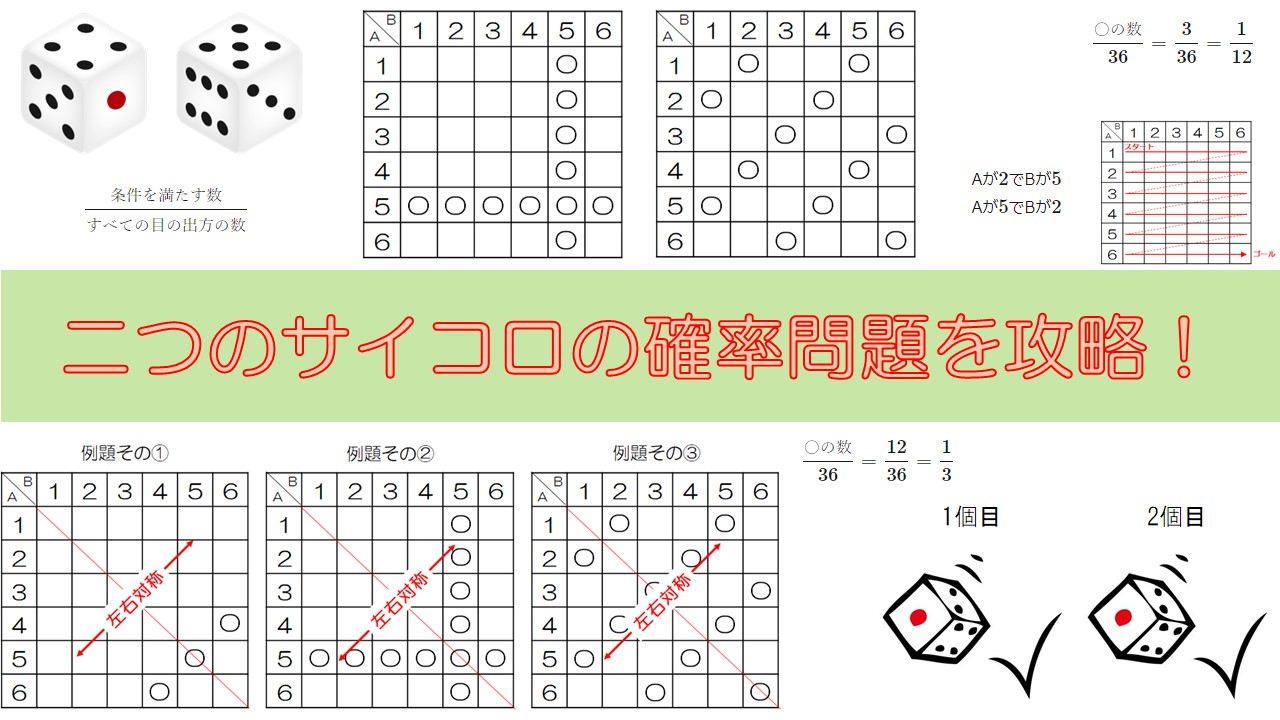
中学2年数学 確率 二つのサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト

第2学年 6 確率 知識・技能の習得を図る問題 年 組 号氏名 練習問題① 1 次の(1),(2)の各問いに答えなさい。 (1) 投げたとき，表になる確率が である硬貨があります。「数学が苦手で、特に確率が苦手だ」 「共通テストでも確率がネックで点数が安定しない」 「二次試験で確率が出たら捨てるようにしている」 などなど、確率は受験生をもっとも苦しめる数学の分野ではないでしょうか？ この記事では、Русский ·соединяя в себе значения предлогов «из» и «за», обозначает направление действия или движения откудалибо и притом с обратной или с другой, противоположной, стороны чеголибо

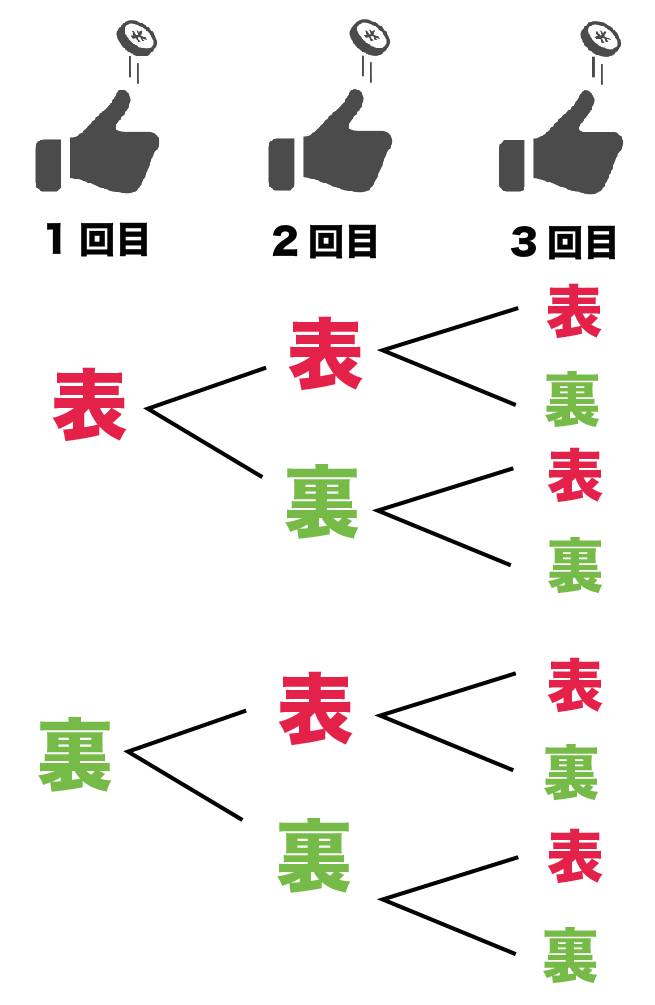
 確率の公式・計算式は正直、たくさんある。 だけど、中学数学ではたった1つの公式で大丈夫。 どんな確率問題もとけるようになるんだ。 あることがら「A」がおきる確率の求め方は、 つぎの公式で計算できちゃうよ。 （Aが起きる場合の確率） = （ことがらAが起きる場合の数）÷（すべての場合の数） だ。 もうちょっと公式っぽくしたい。 そんなとき2．単元の目標 （1）日常生活の中での不確定な事象について，確率を用いて考察しようとする。 関心・意欲・態度 （2）起こり得る場合を順序よく整理したり，不確定な事象の起こる程度を数値化したりすることを通して，事象を数理的に考察することができる。 見方や考え方 （3）樹形図や表を利用して場合の数を数えたり，いろいろな場合についてのA,\B A, B を決めると， A = 1 1 − α N, B = − α N 1 − α N A=\dfrac {1} {1\alpha^N},\B=\dfrac {\alpha^N} {1\alpha^N} A = 1− αN 1 , B = 1− αN −αN となる： a n = α n − α N 1 − α N a_n=\dfrac {\alpha^n\alpha^N} {1\alpha^N} an

最初の数が1のとき目の和が5になるのは、(1, 1, 3)、(1, 1, 3)の2通りです。 最初の数が2のとき、合計が一番小さくなるのは(2, 2, 2)の組み合わせですが、これでは問題の条件である5より大きなってしまいます。 よって、条件を満足するのは、最初の数が1 である2つの場合だけであることがわかります。 ・組合せ (1, 1, 3)のとき、順列は 通り。 ・組合せ (1, 1, 3)のとき Usage notes The preposition, изза in the sense of "stating the cause", has a negative connotation pertaining to the noun in question This is opposite to the preposition, благодаря́ (blagodarjá), that has a positive connotation The preposition изза in the sense of "stating the cause" has a similar connotation with the prepositions по (po) (with a dative noun)さいころ2個は表を使って考えよう！ さいころの確率問題では このような6マス×6マスの表を使って考えると とーっても分かりやすいからおススメです！ この表の見方としては タテとヨコをそれぞれ 大きいさいころ、小さいさいころの目だと考えて見

センター数学 Aの確率問題に不備か コインの裏表の出る確率が記載されていない いままでサイコロのときも書いてなかった まとめダネ

中学数学の確率の問題の解き方 コイン サイコロ くじ カード 数学fun

 中学数学の確率は、マスターすれば簡単です。 正しいやり方さえ身につけられれば、得点源にできるでしょう。 参考：確率以外も含めた中学数学の勉強法はこちら 数学が苦手な中学生の勉強法 確率の問題を・・・ 中学数学（確率編）場合の数が分かれば確率が分かる 実際に使って覚えよう 公式を理解して、覚えるには実際に使ってみるのが一番です。 簡単な問題からはじめよう まずは、簡単な確率の問題を例にします。 確率の問題① 一つのサイコロを振って2の目が出る確率を求めなさい。 という問題を考えてみましょう。 みなさん、 「こんなの考えるまでも P (A) = 事象Aが起こる確率 P (A)の求める公式は以下になります。 事象 が起こる場合の数 起こりうる全ての場合の数 言葉の定義だけだと分かりづらいですよね。 以下では実際の問題を解きながら、この公式が意味するところを丁寧に説明していきます。 確率の問題は、公式に当てはめれば解ける分野ではありません。 自分の頭でしっかりと理解することが

サッカー日本 ポーランド戦 ラストの時間稼ぎは数学的に正解 予選突破の確率を分析した結果 攻めた場合を上回る ねとらぼ

高校2年生数学 進研模試対策 条件付き確率 土曜補習プリント 赤城 ᐡᐤᐡ

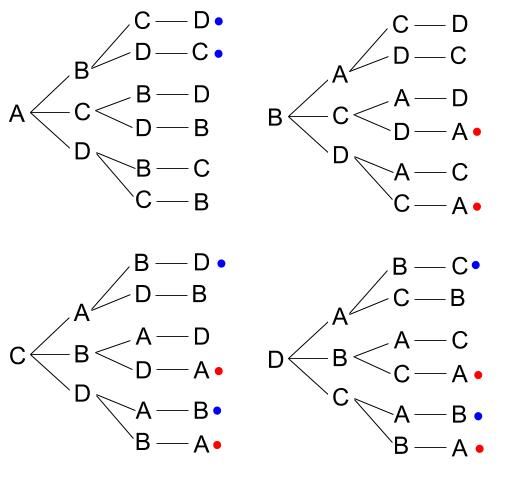
場合分けを要することが多い もう1つの難しさに「場合分け」がある。 これは抽象的な話をするよりも、例を挙げて説明した方が早い。 上の＜例題2＞ を例にしよう。 2つのサイコロの積が6の倍数ということは、 片方が2の倍数かつ他方が3の倍数 片方が6の倍数 という 2つのパターン が考えられる。 少し考えれば分かることだが、この2つは一本の式でまとめて確率の求め方とは？ 全体分の求める数です 確率をしっかりマスターしたいと思ったら？ 確率の求め方とは？ 全体分の求める数です まず、確率における基本中の基本を 2 2 つまとめておきます。 確率とは何か → 確からしさの度合い。 事象の起こりやすさ。 たとえば、「サイコロを 1 1 回投げたとき、 3 3 以上の目が出る確率」であれば、 4 6 = 2 3 ≒通り 通り 通り 通り となります． 2A，B，C，D，E，Fの6人の中から2人の委員を選ぶとき，選び方は何通りあるか． *1 解答1 書き出す解き方 今回の問題は アルファベット順 に書き出します．つまりB→Cは可，E→Aは不可であるということです． 通り 解答2 組み合わせの解き方 選択の問題は順列から「カブり」を取り除くことで求めることができます． (AB)と

中学数学 確率の問題を攻略できる5つのコツ Qikeru 学びを楽しくわかりやすく

高校数学a 最大値 最小値の確率 受験の月

確率の基本 ※数学Aで習う確率の初めの部分は，中学校の復習になっている． 確率の定義 例1 くじで当たる確率を求めるときに，「当たりかはずれかどちらかだから，当たる確率は2分の1」などと雑な議論をしてはいけない． 数学が好きで興味がある人 or 大学で「ベイズの定理」を習った人はもしよかったらご覧ください。 wwwmomoyamausagicom 6．練習問題 では、重要な5つの法則を復習するために練習問題にチャレンジしてみましょう。 練習1 5本のくじがあり、そのうち2本が当たりである。 くじを同時に2本引いた高校数学A「場合の数と確率」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 「場合の数」に関する34のポイントを覚える 「確率」に関する18のポイントを覚える まずはこれらのポイントをしっかり覚えてから、例題や練習にある問題を解いて「場合の数と確率

確率 統計 応用数学基礎講座 絵本ナビ 岡部 靖憲 みんなの声 通販

数学a基礎 場合の数と確率 整数の性質 解説 例題コース 最新刊 無料試し読みなら漫画 マンガ 電子書籍のコミックシーモア

Amazonで森岡 毅, 今西 聖貴の確率思考の戦略論 USJでも実証された数学マーケティングの力。アマゾンならポイント還元本が多数。森岡 毅, 今西 聖貴作品ほか、お急ぎ便対象商品は当日お届けも可能。また確率思考の戦略論 USJでも実証された数学マーケティングの力もアマゾン配送商品なら通常 Группа НАНА — легендарная российская группа, созданная знаменитым продюсером и рокмузыкантом Бари Алибасовым НАНА совершила своеобразную сексуальную революцию в России В составе группы НАНА попрежнему первыеただ数学において確率を問われた場合、「 ％」と答えるのではなく分数で答えないといけないので『1を6等分して\(\dfrac{1}{6}\)』と考えましょう。 では確率の問題を解いてみましょう。 確率の練習問題 問題1 サイコロを振った時、出る目が3以上である確率を求めよ。 サイコロの出る目は全部で

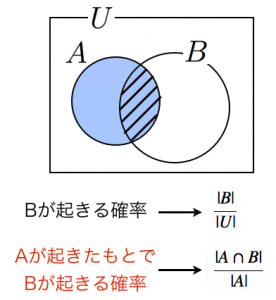
条件付き確率の意味といろいろな例題 高校数学の美しい物語

中2 中２ 数学 確率まとめ 中学生 数学のノート Clear

今回は、中学・高校数学で学習するレベルの確率から 『くじ引きの確率』 について解説していきます。 取り上げるの次の問題 ~くじを戻さない~ 当たりくじを3本含む10本のくじがある。このくじをa、bの2人が順に1本ずつ引く。ただし、引いたくじは 元に戻さない ものとする。 （1）aが当たるEnjoy the videos and music you love, upload original content, and share it all with friends, family, and the world on確率の定義とは、全事象U、事象Aの要素の個数をそれぞれn (U)、n (A)とする。 全事象Uの根元事象が同様に確からしいとき、事象Aの起こる確率P (A)は以下の式になる。 この定義さえ理解していれば確率が理解できるようになると思います。 さらに確率の計算をするときは同じものでも区別する必要があります。 例）赤が3つある場合は、赤1、赤2、赤3のように区別し

条件付き確率とは 公式を使ってサイコロ 玉の問題を解いてみよう くじ引きを用いた例題付き 高校生向け受験応援メディア 受験のミカタ

高校数学a 反復試行の確率 基本 Ncrp R 1 P N R 受験の月

 最小二乗法の行列表現： 主張1：行列 A A A と列ベクトル b undefined \overrightarrow {b} b が与えられたときに ∥ A x undefined − b undefined ∥ \A\overrightarrow {x}\overrightarrow {b}\ ∥Ax − b ∥ を最小にする x undefined

高校数学a 原因の確率 時間的に逆行する条件付き確率 受験の月

第1回全統記述高3模試数学 確率 過去問練習問題 赤城 ᐡᐤᐡ

朝倉数学大系 １５ 確率幾何解析の通販 砂田 利一 堀田 良之 紙の本 Honto本の通販ストア

楽天ブックス 本当は面白い数学の話 確率がわかればイカサマを見抜ける 紙を100回折ると宇宙の果てまで届く 岡部 恒治 本

確率分布 分散の計算公式の使い方 数学b 定期テスト対策サイト

中学数学 確率 確率の求め方 たった1つの公式ですべてわかる Youtube

中学数学単元別 確率 数学 中学校 教材 問題集 7 学林舎 通販 Yahoo ショッピング

高校数学 確率 玉が登場する確率問題の解き方 数学の面白いこと 役に立つことをまとめたサイト

中学2年数学 確率 確率の求め方 たった1つの公式ですべてわかる 数学の面白いこと 役に立つことをまとめたサイト

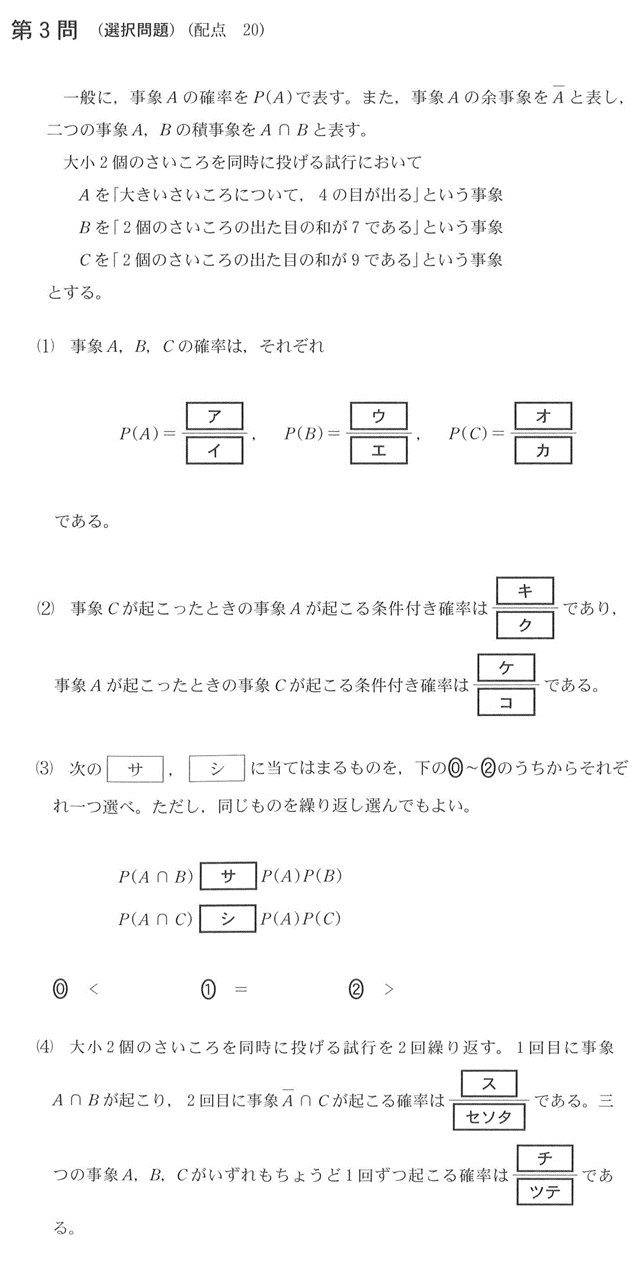
センター試験 場合の数と確率 の必勝テクニック 第3回 応用編 高校生３分ニュース 進研ゼミ高校講座

改訂版 クリアー数学ａ P119 ７ 確率の基本性質

高校生 数学a 東京書籍 1章2節 確率 節末問題 赤城 ᐡᐤᐡ

1

世界一わかりやすい数学問題集中２ ６章 確率

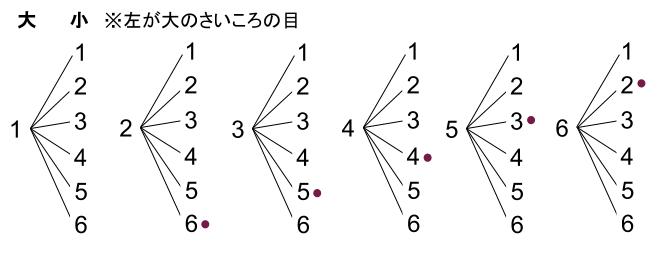
中学数学 確率 さいころ 中学数学の無料オンライン学習サイトchu Su

数学 中2 84 確率チャレンジ Lv 6 カード編 Youtube

これで点が取れる 単元末テスト中２数学 ６章 確率

確率分布と統計的な推測 攻略本 センター数学iib第5問を紐解く 朝盈夕虚 Booth

3

確率 怜悧玲瓏 高校数学を天空から俯瞰する

数学a 確率を球に関する問題で考えるチャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru

数学 確率統計デイシステムトレード ロジック説明ファイルとea インジケーター 電子書籍 自動売買 相場分析 投資戦略の販売プラットフォーム Gogojungle

高校数学a 反復試行の確率 先にk回起こる 受験の月

中学２年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

サイコロの確率の問題 京極一樹の数学塾

数学a基礎 場合の数と確率 整数の性質 解説 例題コース 漫画 無料試し読みなら 電子書籍ストア ブックライブ

中学2年の数学 動画 確率まとめの問題 19ch

確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ

やさしい条件付き確率の問題 ２０２０年度前期日程の茨城大学教育学部数学教育入試より 身勝手な主張

数学 中2 85 確率チャレンジ Lv 7 まとめ編 Youtube

技術者のための確率統計学 大学の基礎数学を本気で学ぶ Seshop Com 翔泳社の通販

高校数学a 組合せ の確率2 応用 例題編 映像授業のtry It トライイット

場合の数 Of 京極一樹の数学塾会員頁

中学2年数学 確率 二つのサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト

統計と確率 リフレッシュ数学５ 黒田孝郎著 遠山啓 矢野健太郎監修 高山文庫 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋

センター試験 場合の数と確率 の必勝テクニック 第1回 基礎編 高校生３分ニュース 進研ゼミ高校講座

くじ引きの当選確率を計算できますか 中学数学が日常生活に役立つ例 2 オンスク Jp

中学2年数学 確率 カードが登場する確率の問題の解き方 数学の面白いこと 役に立つことをまとめたサイト

受験 定期試験 数学解き方集 裏技 解法 確率応用 高校数学

中学2年数学 確率 場合の数を求める問題の解き方 数学の面白いこと 役に立つことをまとめたサイト

高校数学a 期待値e X 受験の月

数学を分かりやすく考えてみようと試みるサイト 分かりやすい高校数学 確率 4 数え上げの条件

改訂版 ４プロセス数学ａ P134 ８ 条件付き確率

書籍紹介 確率論 福島正俊 著 数学

16年前期 千葉県公立高校入試 数学 第2問 4 確率 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

数学場合の数 確率分野別標準問題精講 旺文社

高校数学a 条件付き確率pa B と通常の確率p A の違い 受験の月

1

中学2年数学 確率 場合の数が分かれば確率が分かる 数学の面白いこと 役に立つことをまとめたサイト

中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく

高校数学a 順列 の確率2 応用 練習編 映像授業のtry It トライイット

高校数学a 組合せ の確率1 基本 例題編 映像授業のtry It トライイット

新装版 経済数学教室 9 確率論 岩波オンデマンドブックス 小山 昭雄 本 通販 Amazon

高校数学 問題検索 数学a 場合の数と確率 確率の基礎 数学

数学 中2 81 確率チャレンジ Lv 3 コイン編 Youtube

高校数学無料問題集 数ａ 第１章 場合の数と確率 条件付き確率 桝 ます Note

高校数学a 和事象の確率 の求め方1 加法定理 映像授業のtry It トライイット

数探高校講座 数学a 場合の数と確率 8 独立な試行の確率 数学探究所

中学２年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

高校数学無料問題集 数ａ 第１章 場合の数と確率 条件付き確率 桝 ます Note

高校数学a 組合せ の確率2 応用 練習編 映像授業のtry It トライイット

数学 中2 79 確率チャレンジ Lv 1 基本編 Youtube

確率 立命館 理系全学部 19 2 2数学 経済学 統計学 オンライン指導

中2 中2数学 確率 中学生 数学のノート Clear

コンプリート 数学 確率 問題 ぬりえのベストコレクション

1

技術者のための確率統計学 大学の基礎数学を本気で学ぶ 中井 悦司 翔泳社の本

面白い数学の問題 トランプがダイヤである確率 早稲田大学の入試問題が中学生でも解ける そらの暇つぶしch

思考力を鍛える場合の数と確率 分解 と 統合 でみるみる身につく 書籍案内 技術評論社

確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ

中学 確率 完全攻略 中学生 数学のノート Clear

中学 確率 完全攻略 中学生 数学のノート Clear

楽天ブックス 確率 統計第2版 工科の数学 田代嘉宏 本

確率２２ 鯉のぼり問題 怜悧玲瓏 高校数学を天空から俯瞰する

國二 Junior High数学的確率 筆記 Clear

確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ

Amazon Co Jp １０秒でわかる 高校数学１ａ 場合の数 確率 の考え方 江間淳 Ebook 江間淳 本

大学入試センター試験 数学 確率 154 数学 さくら教育研究所 Skredu

中学数学 確率 人を並べる 人を選ぶ 中学数学の無料オンライン学習サイトchu Su

高校数学a 反復試行の確率1 ちょうどｎ回の確率 映像授業のtry It トライイット

数探高校講座 数学a 場合の数と確率 3 順列 数学探究所

改訂版 3trial数学a P113 ８ 条件付き確率

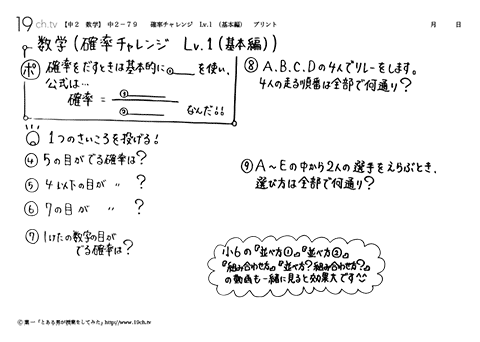
中学2年の数学 動画 確率チャレンジ Lv 1 基本編 の問題 19ch

高校数学 数ａ ２７ 確率 くじ編 Youtube

数学a確率一般の和事象の確率の問題です 2 2 3c2 Yahoo 知恵袋

場合の数と確率 条件つき確率の解き方について 数学a 定期テスト対策サイト

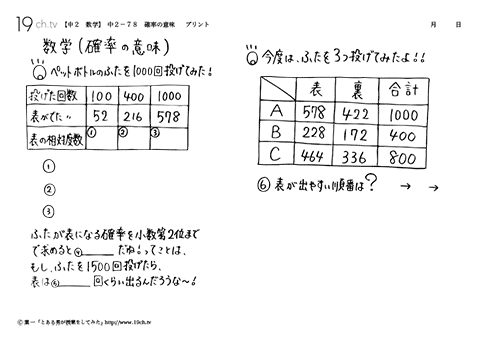
中学2年の数学 動画 確率の意味の問題 19ch

数学ガールの秘密ノート 確率の冒険 数学ガールの秘密ノートシリーズ 結城 浩 本 通販 Amazon

中2 中2数学 確率 中学生 数学のノート Clear

数学a基礎 場合の数と確率 整数の性質 演習コース 数学a基礎 演習コース 石井大裕 数学 Kindleストア Amazon

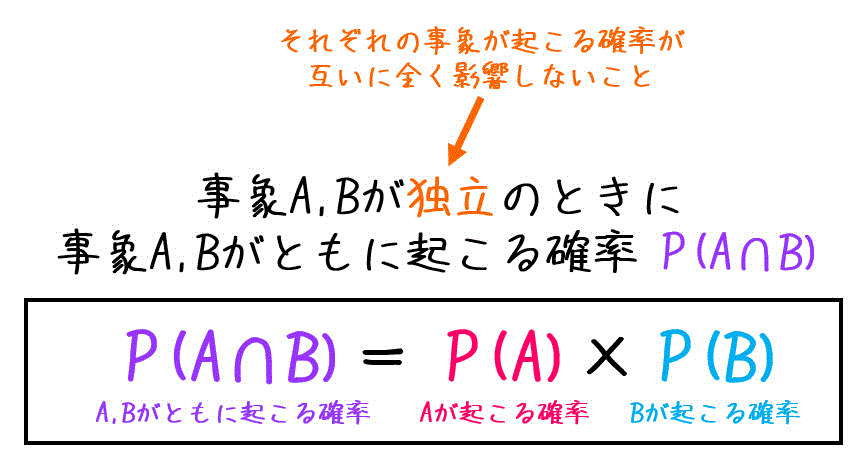
確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾

高校数学 数a １９ 確率 さいころ編part 1 Youtube