分方程式は階数が上がると解くのが難しくなるので階数を下げて連立微分方程式の形に持ち込むということがよ くやられます。余談になりますが,一般に2 階線形微分方程式 d2x dt2 P1(t) dx dt P2(t)x = Q(x) を連立微分方程式にして階数を下げるには, x = x1;X2 = dx dt普通、連立方程式はこのように解きます。しかし連立方程式は、行列によっても解くことが可能です。次に、それについて見ていきましょう。 12 行列を使った解き方 まず、上の連立方程式は、行列を使うと次のように表現することができます。 \

求解釋倒數第二行的連立方程式是怎麼來的 Clear
連立方程式 三文字
連立方程式 三文字-連立方程式の解き方 連立方程式を解くには、主に2つの方法があります。 まず、 代入法 と呼ばれる方法です。 片方の式をx= や y= の形に変えて、それをもう片方の式に代入することで文字を1つ減らし、答えをもとめる方法です。方程式・連立方程式の文章題 が得意になる3倍効率的な勉強法 方程式や連立方程式の文章題:各ジャンル別の問題一覧 食塩水の濃度編 学習はこちら: 濃度に関する方程式と連立方程式の文章題基礎~難問 坂田先生 以下の問題パターンの解法が習得




高校数学で学習する連立方程式の解き方まとめ 数スタ
連立方程式れんりつほうていしき 二つ以上の方程式を組にし,それらを同時に満足する未知数または未知 関数 を求めようとするもの。 未知数の数がm個,未知数に関する最高次数がn次の場合をm元n次の連立方程式という。 一般にm元の連立方程式は連立方程式の例 2元1次連立方程式(以下の文章では「連立方程式」と書くことにします)は例えばこんな形で出てきます。 $$\begin{cases}2xy=4\\ 4x3y=8\end{cases}$$ この情報から、\(x\)と\(y\)の解を出せと言われるのがよくあるパターンです。連立方程式とは 2つ以上の方程式を組み合わせたものを「 連立方程式 」といいます。 このうち、2つの文字を含む1次方程式を組み合わせたものを「 連立2元1次方程式 」といいます。 連立2元1次方程式の例 \(~~~\begin{cases} x2y=10&・・・①\\ 3xy=9&・・・②
連立方程式とは {7x2y =5 2x5y = 8 のように2つ以上の方程式を組み合わせたものが 連立方程式 である。 組み合わせた, どの方程式も成り立たせるような文字の値の組が連立方程式の解となる。 中学で扱うのは上記のような2元1次方程式の連立方程式である。連立方程式の解は、全ての式が同時に成り立つような値でなければなりません。 よって、 変形中に「0= (0じゃない値)」みたいな絶対に成り立たない式が出た時点で解なしが確定する のです。 このようなシチュエーションを拡大係数行列で表すとこのよう連立方程式の電卓 2つの方程式を入力することで連立方程式として解くことができる電卓です。計算方法は加減法または代入法で選択でき、途中式も表示されます。 式の展開の電卓 入力された数式を展開
連立方程式を解け x=2y5 x3y=7 x3y=7 x5y=11 2x3y=8 x5y=11 x2y=4 x3y=7 x2y=10 x=3y5 2x5y=11 3x4y=6 xy=10 x=y4 01x05y=13 03x04y=06 3xy=5 2 (x3y)=14 2 3 x 1 5 y= 8 15 2 5 x 3 10 y= 2 5 1 2 x 2 3 y= 1 6 3 2 x 7 6 y= 13 6 x3y=4x6y=2 連立方程式 (加減法1)_ 例題と練習 連立方程式 (加減3つの文字、式の連立方程式を計算する方法 xy=3,xy=2の和と積の連立方程式の解き方は? 途中で速さが変わる文章問題の解き方、コツを解説! 割合を使った全校生徒の増減に関する文章題の解き方を解説! 池の周りを追いつく速さの問題を解説!←今回の記事2年 連立方程式7/11 教p4445( )年( )組( )名前 a=b=c の形の方程式は,次の3つのいずれかの形の連立方程式に ・ 連立方程式を解くには、既習である文字1つの方程式を導けばよいことに気付くことがで きる。
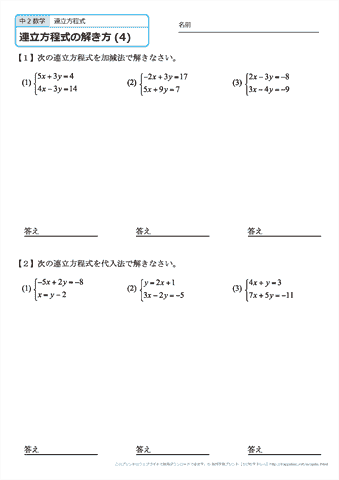



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




連立方程式 連立方程式の加減法と代入法 中学数学 定期テスト対策サイト
ベーシック数学 eテレ 毎週 月曜日 午後2:00〜2:10連立方程式 を解け. (東京都15年) 解説を見る とも係数がそろっていない. の係数をそろえるには, (1)式を5倍, (2)式を9倍するとよい. ※こんな分数の答えになってしまったら,合っているかどうか心配になるが,検算して成り立っていれば連立方程式の利用を解くには、大きくわけて3段階あります。 ①かけ算・わり算の文章題を解ける ②文字を式で表す(個数と代金)ことができる〈中1生1学期範囲〉 ③連立方程式の利用(個数と代金)を解ける〈中2生1学期範囲〉 上から一つずつ確認して



連立方程式の文章題 パーセント チーム エン




方程式練習問題 連立方程式の文章問題 道のり 速さ 時間 方程式の解き方まとめサイト
連立方程式は、複数の変数または寸法を同時に解くリレーションです。 連立方程式を作成する場合は、次の規則に注意してください。 • 連立方程式で使用されている変数は、方程式の先頭で宣言しなけれ今回は連立方程式の文章問題の中でも、中学生が苦手としているトンネルの問題の解説をしていきます。 基本的な考え方はカンタンですので、頑張って理解してくださいね! 連立方程式 トンネルの問題連立方程式の解き方は、下記の2つがあります。 加減法 ⇒ 1つの未知数が消えるように2つの方程式を加減し、もう一方の未知数の解を求める方法 代入法 ⇒ 1つの式を「x=」の形にして、もう一方の式に代入し解を求める方法 加減法、代入法の詳細は、下記




4元連立方程式を解く際に気をつけるべきポイントは何でしょうか Clear



第1章 連立方程式
連立方程式 110 /41件 表示件数 5 10 30 50 100 0 1 0325 男 / 歳代 / 高校・専門・大学生・大学院生 / 非常に役に立った / 使用目的 検算 ご意見・ご感想 アルゴリズムで解いている以上,分数表示などはできないのかなと思います定価・原価・利益の問題(連立方程式) 問題文の中に、求める数が2つある場合は、それぞれを 、 で表します。 ただし、問題によっては、求める数に関連のある数を 、 としたほうが解きやすい場合もあります。 問題文から等しい関係にあるものを2 次の連立方程式が同じ解をもつという。 (1)同じ解を求めなさい。 (2) a, b の値を求めなさい。 { −4 =25① 2 −y=8 ② {2 8 =−14③ −3 2y=−13 ④ 同じ解をもつので,その解は②④の解 そこで,②④を連立方程式で解く。




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



Q Tbn And9gcsm6 Ygdifx7pydebyfkxkcficln0q2usbh7vlhkbagbczf8kws Usqp Cau
2章 連立方程式 求めたい数量が 1節 連立方程式 とができる。 とその解き方 2 1 の解 している。連立方程式と その解 1 1 について考える 連立方程式の必要性 を理解する。 ・3 点シュートと2 点シュートの連立一次方程式の解を求める方法には、掃き出し法があった。 逆行列① (簡約化) 例題を解きながら逆行列を簡約化を用いて求める方法をコツを交えながらわかりやすく解説します。 逆行列は行列の逆数に相当する概念であり、定義とその求め方の両方を『連立方程式』の単元から 連立方程式を 代入法で解く方法 について解説していくよ! 連立方程式を解くためには 『加減法』と『代入法』という2つの解き方があったよね。 でも 加減法は分かるけど、代入法は苦手




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu




例題付き 連立方程式の解き方と失敗しないコツ
大変シンプルですが、シグマ、偏微分、連立方程式、行列などの要素が登場します。 計算器と数学のコラボレーションとしてもとても面白いです。 なるべく平易に、カジュアルにまとめてみます。 プログラミング環境 環境は、openframeworksを使います。連立線形微分方程式 {x ′ = ax by y ′ = cx dy について いずれか一方の関数の線形2階斉次微分方程式に帰着させて解くことができるようになります。 微分演算子を用いた表現により,連立方程式を解くことができるようになります。 係数行列の対角化にこの形の方程式を解くとき,普通の方程式を解くときの 「移項」のような変形をしにくい ので,解き方のコツを覚えておくとよいでしょう. 〇「 A=B=C 」というのは,「 A=B かつ B=C 」を省略的に書いたものです.だから,「 A=B=C 」という方程式が与えられ



Q Tbn And9gcqmqld3xsadaykot52ts2j9chbiy4x Ibxise3r9lkufnxidis Usqp Cau



Q Tbn And9gcr6u7wiu1vwagawevsokbm01ikg28bm5v2qbikureakvo9g6v9k Usqp Cau




連立方程式と解 On Vimeo



中2第2章29連立方程式の利用 解と連立方程式
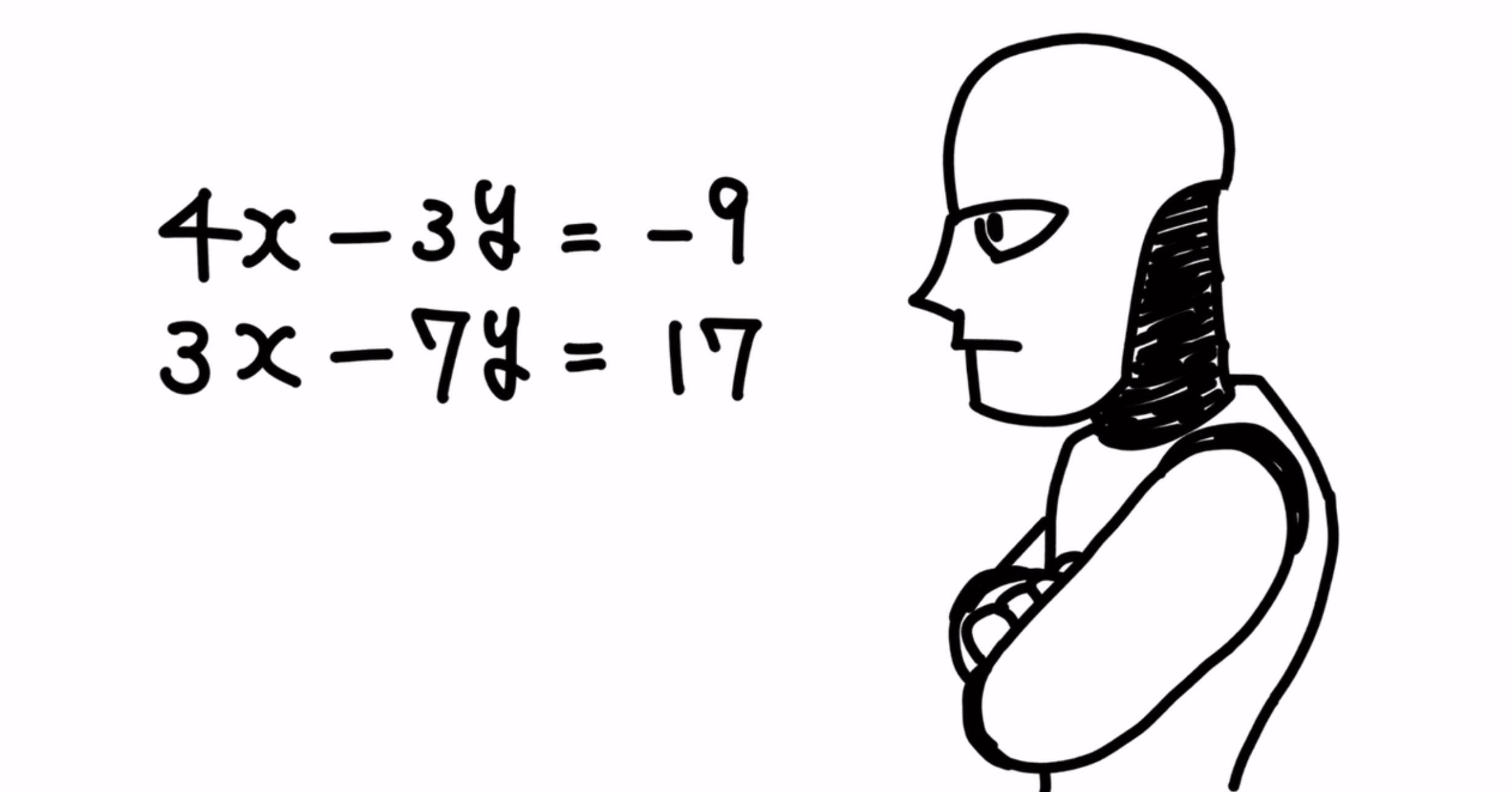



Aiは連立方程式を どうやって解くか Mucun Wuxian Note
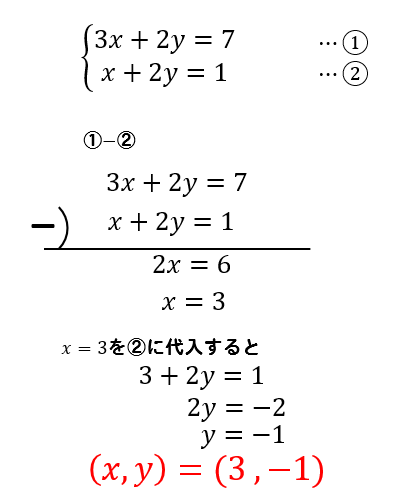



方程式の高校入試問題 連立方程式 方程式の解き方まとめサイト




連立方程式を ノート上で どう解いていくか ページ 7




小数の連立方程式の解き方 両辺を10倍や100倍しよう 中学や高校の数学の計算問題




連立方程式の解き方 加減法 2 Youtube




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者



3 Y Shop Clothing Shoes Online



たかが連立方程式ではあるけれど 大験セミナー わくわく日記



第1章 連立方程式




数学 連立方程式 速さの問題 Youtube




中2 連立方程式3 解き方2 中学数学の勉強に




連立方程式 計算 Apk Download For Android Latest Version 1 2 Com Simul




Mr Neo Math 22 P07 On Vimeo




連立方程式の解を代入 Youtube




方程組 維基百科 自由的百科全書



測評網 國一下 數學第一次段考 複習錦囊




連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト




三元一次聯立方程式線性聯立方程式 Ropux




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット



Studydoctorかっこのついた連立方程式 中2数学 Studydoctor




中2数学 連立方程式の加減法2 係数をそろえる 例題編 映像授業のtry It トライイット




高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月
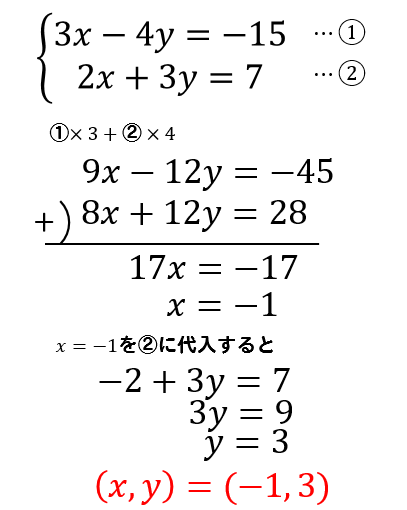



連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ




Rimg0010 連立方程式を解くウィルバーマシン Masakazu Takahashi Flickr



三石 数学塾 連立方程式が解けないとき




Tomas Mollerの交差判定 基礎編 試行錯誤




中学数学 連立方程式 の効果的な教え方 小数 分数問題



Q Tbn And9gctdm2ioiwx1ofwk6oxyprfslnkssmzd2jo K6eubdtv2cctnoej Usqp Cau




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




トップ100連立方程式公式 最高のカラーリングのアイデア




中2 中2 連立方程式 授業ノート 中学生 数学のノート Clear




Tiktok 上的 連立方程式標籤影片




数学の一問一答 連立方程式 勿忘荘
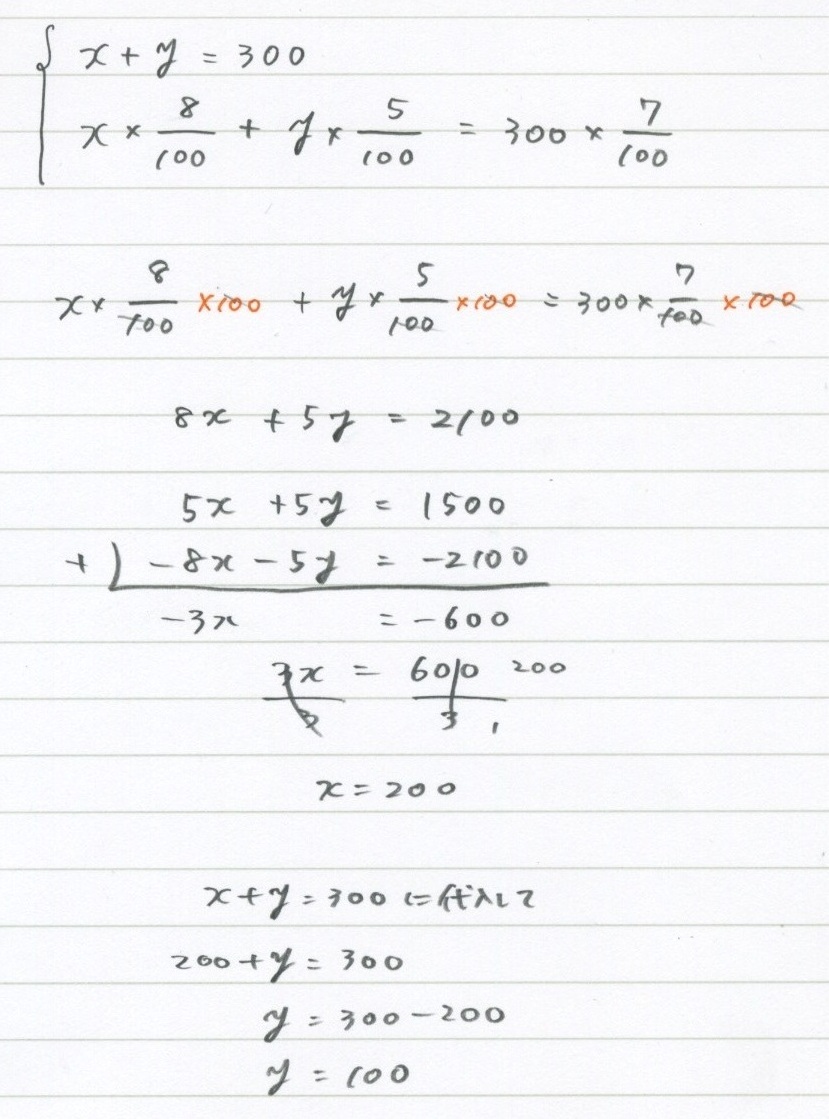



5 3 連立方程式 食塩水 勉強できようサイト




連立方程式の解き方を説明しますー代入法を使った解き方ー おかわりドリル




連立方程式の文章題2 割合に関する問題 無料で使える中学学習プリント




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト
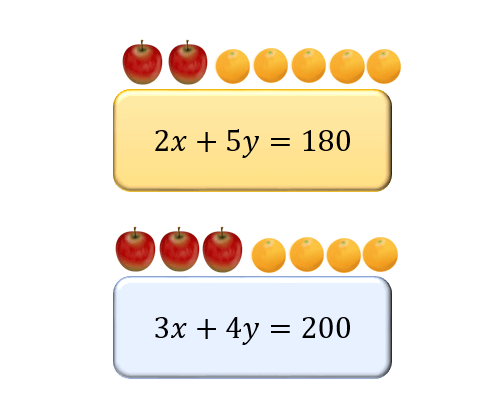



連立方程式 加減法 の解き方 なぜ加減法が成り立つか アタリマエ




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Introduction To Numerical Analysis For Python No2 Matrix And Simultaneous Equations Japanese Edition Yutaka Shirai Ebook Amazon Com



連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料




連立方程式 Yを消す Math Algebra Solving Equations 7th Grade Math Showme
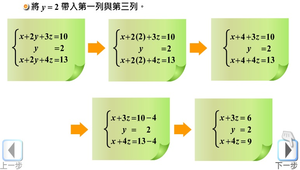



高斯消去法解三元一次聯立方程式




この連立方程式の解き方を教えてほしいです Clear



連立方程式 Latex




連立方程式 問題 Youtube




ちょっと複雑な連立方程式を練習しよう インターネット家庭教師のアスミラ



名師課輔網 係數對稱的聯立方程式



連立方程式の行列解
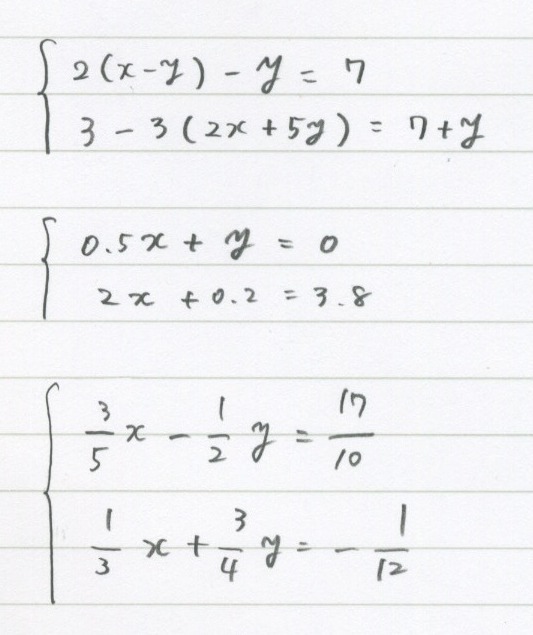



5 2 連立方程式 かっこや分数小数はもうできる 勉強できようサイト




25 3 連立方程式 ニスヌーピー壁紙




連立方程式の問題 高校の範囲でも登場する大切な分野だ 中学や高校の数学の計算問題




高校数学 3元連立1次方程式 一般型と循環型 受験の月
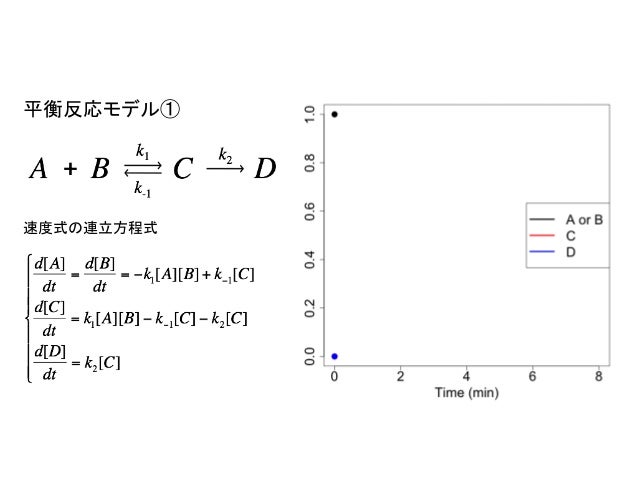



R Note Ode Ver1 0




連立方程式計算安卓下載 安卓版apk 免費下載




P4 1加減法 公立高校入試問題 かずお式中学数学ノート8 中2




連立方程式の解き方 加減法 1 Youtube




例題 二元一次聯立方程式的解 數學 均一教育平台



課程介紹 二元一次聯立方程式 發現學習的美麗新世界



連立方程式 その1 名古屋市北区の学習塾は思考力を育む 泰成スクール



測評網 國一下 數學第一次段考 複習錦囊




無料ダウンロード中1 方程式文章問題 最高のカラーリングのアイデア




お勉強 連立方程式を楽に解く 数学は楽してなんぼ そらの暇つぶしch




高校数学で学習する連立方程式の解き方まとめ 数スタ




Pythonで汚い4元1次連立方程式を解いてみた




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




連立方程式とその解 まなびの学園




中2数学 連立方程式の文章題 割合 練習編 映像授業のtry It トライイット
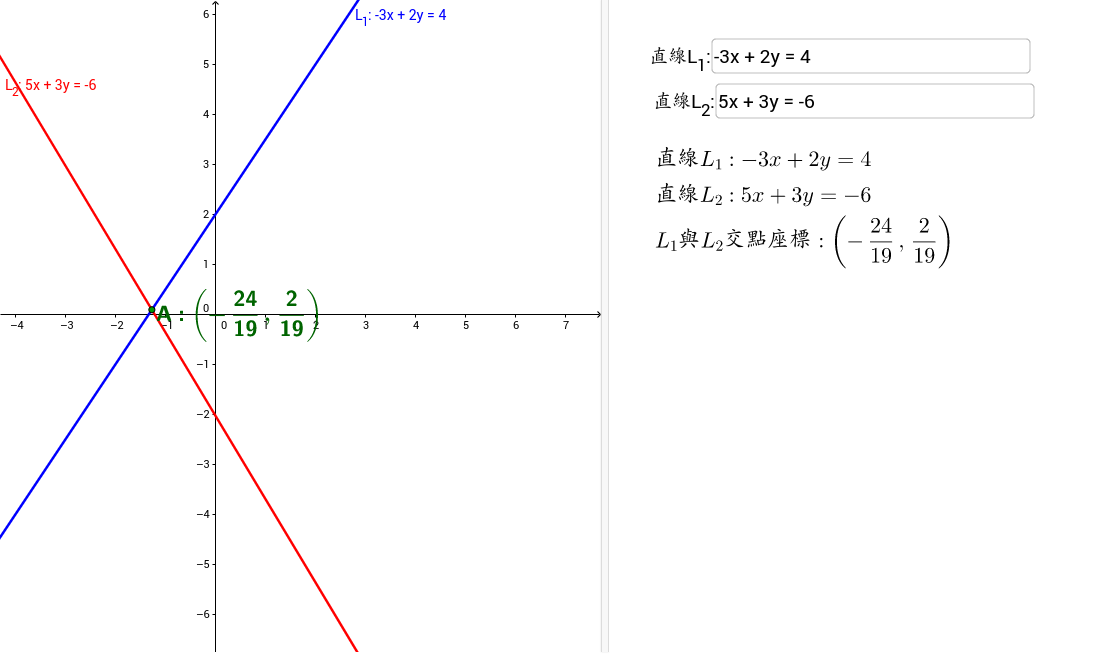



二元一次聯立方程式圖解 Geogebra




求解釋倒數第二行的連立方程式是怎麼來的 Clear




二元一次聯立方程式公式解 1下數學 魔術方塊and數學 隨意窩xuite日誌




連立方程式みかんとリンゴ加減法のしくみ Youtube




國二junior High数学的連立方程式の文章題筆記 Clear




連立方程式の表し方 Geogebra




連立方程式計算安卓下载 安卓版apk 免费下载




中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム




数学 中2 15 連立方程式 加減法の基本編 Youtube




中学2年生 数学 無料問題集 連立方程式を加減法で解く おかわりドリル




二元一次方程式的圖形ax By C 的圖形y K 的圖形x H 的圖形二元一次聯立方程式的圖形自我評量 Ppt Download




九元連立方程式求解機 解説ビデオ Rikazo Flickr




連立方程式 加減法 計算ドリル 問題集 数学fun




Excelによる簡単な線形代数 Ipl Cs Is Nagoya U Ac Jp 連立方程式の解法連立1次方程式の解法は直接法と反復法に分




Rank Of Matrices And Homogeneous Linear Equations




例題 解二元一次聯立方程式 綜合應用1 數學 均一教育平台




翻轉學習影片 國中 數學 4 2 2 解二元一次聯立方程式




Junior High数学的中2 連立方程式筆記 Clear




中2数学 連立方程式の文章題 割合 例題編 映像授業のtry It トライイット




連立方程式の2つの解き方 代入法 加減法 数学fun




連立方程式 加減法 無料で使える中学学習プリント




連立方程式の解き方 加減法 代入法と文章題の計算方法 リョースケ大学



0 件のコメント:
コメントを投稿