[10000印刷√] 多項式 展開 242827

如果他们具有相同的喜恶（五阶导数值相同），具有相同的三观（六阶导数值相同），那么用李四替代张三就越来越合理了。 这也是为什么泰勒公式展开越多项，在展开这一点的附近就越接近f (x)本身。 现在再看一眼公式，大家能「理所当然」地理解为啥泰勒可能除得盡：餘數是零，商數是多項式。 可能除不盡：餘數不是零，商數是無窮多項式。 展開 多項式的連乘、多項式的次方，化作一個多項式。 f(x) = 2x⁰ (2x⁰ 1x¹) (2x⁰ 2x¹ x²) = 8x⁰ 4x¹ 0x² 2x³ f(x) = (2x⁰ 1x¹)² = 4x⁰ 4x¹ 1x² 分解 展開的反方向。 → jovi72數學、3d繪圖、多項式展開、除法等都有，連線上轉pdf都有 10/28 2230 推 jovi72 還有一些奇奇怪怪的數學工具，但好像沒有2D繪圖，有點美中 10/28 2234

特征多项式展开公式 二十世纪最伟大的十大经典算法 学习岛

多項式 展開

多項式 展開-1 泰勒展開：多項式逼近函數 多項式是一個很棒的函數，好處之一是它可以求導無限多次。這種函數應該發予良⺠ 證，實在太棒了！不過就這點而言還不夠特別，指數函數、三⻆函數也都可以發予良⺠證。 多項式還有一個好處是比較好代值，譬如說p(x)˘x23 ¡5x18展開下列多項式，並按變數的降冪排列表示答案。 4 ((a) 4x3)(x−2) ( (b) 2−3x)(2x3) 5 )(a) (−6y5(9−4y) ( (b) 9−2c)(37c) P 8 中一級數學工作紙 – 第7 章 簡易多項式的運算 展開下列多項式，並按變數的降冪排列表示答案。 6 ((a) x2−2x

Cf 934d 数学推导多项式展开 Linfanty的博客 Csdn博客

L h @ 4 對定值x而言，函數的精準度會隨著多項式的次數n的增加而增加。 對一個固定次數的多項式而言， 確度隨著x離開x=0處而遞減。 精Algebra－多項式的部分分式技巧 簡介：部分分式（Partial fraction decomposition），是將 有理函數 分解成許多次數較低有理函數和的形式，來降低分子或分母 多項式 的次數。 分解後的分式需滿足以下條件： 分式的分母需為不可約多項式（irreducible polynomial）或其形abcd面積以x的多項式表示，並以降冪方式排列。 Ex 4：已知(x 2 mxn)(x 2 −x u)展開後，x 3 項和x 2 項係數均 為0，求m、n。

多項式的處理與分析 本章介紹matlab處理多項式的相關指令，以便用於多項式的計算與分析， 包括：多項式的加、減、乘、除、求值、求根、微分、積分、矩陣的特徵多 項式、部份分式展開、多項式擬合等。X l L Í x h j!X=0 x = 0 で定義されていないのでマクローリン展開できません。 そこで， log ⁡ x \log x logx を x = 1 x=1 x = 1 で テイラー展開することを考えます（ x = 2 x=2 x = 2 など別の値でも展開できますが，きれいな式にはなりません）。 これは（平行移動して考える

部分分式 法蘭克 所有實係數多項式的集合我們記為Rx，在這個集合上我們可以定義加法與乘法，這些運算結構使Rx構成所謂的環．實有理函數形如f(x) = P(x)/Q(x)，其中P(x);Q(x)是實多項式且Q(x)不是零多項式．而所有實係數有理函數所構成的集合我們記為R(x)在R(x)中，我們定義E 領導係數：多項式中最高次項之係數(不為0)稱為此多項式之領導係數。 f 次數：當an≠0 時，稱此多項式為n次多項式，記為：deg f(x)=n。 g 單項式：只有一項的多項式稱為單項式。 h 常數多項式：若一多項式僅含常數項a0，則稱此多項式為常數多項式。二項式定理 在國中曾學過二項和的平方公式為 ，但對於二項和的立方公式如 則未學過公式，但我們可以利用 來找出結果如下： 我們想知道如果要推廣二項和的四次方、五次方或更一般的二項和之n次方， 它的展開式是否有一般的公式呢？ 我們再往下看

常用泰勒公式及展開小專題 人人焦點

整式の乗法 多項式の展開公式 小テストno ３の解答 保谷高校数学科

A 將 寫成一 之乘冪，並如前之推導，則可得 。（4） 此為唯一的次數不超過 之多項式滿足 我們便將（4）式右側之多項式稱為 在 之 次泰勒多項式，並以 表之。 a 例 1 求 sine 函數在 之 4 次泰勒多項式 第八章 多項式之應用 對於多項式MATLAB也提供許多指令可供運算，相關的指令如下表： 將根轉為多項式 部份展開式之餘數 多項式中，主要以其係數組成一向量作為運算之基礎。 多項式之通式可表示如下： 其中x 為變數，n為其最高之階，為變數x之次方。 而整式展開とは逆の、 因数分解機 多変数版 もあります。 高速に計算したい場合は、x についての式を因数分解する 因数分解機 もあります。 ツイート 「すぐ使える便利ツール」一覧に戻る

数学千题训练之九多项式的乘法

圖說微積分 五 特殊級數 台部落

L0 的泰勒展開式 當n=1： P 5 x ;1 Ex, n=2： P 6 x ;1 Ex E 5 6 當 x 6, 因此 P n x ;1 Ex E 1 2!例題2 設(1x)n之展開式中，按x的升冪排列，第5,6,7 項的係數成等差數列， 則n=？Ans：7 或14 例題3 (1＋x2)＋(1＋x2)2＋(1＋x2)3＋＋(1＋x2)的展開式中，x4的係數為 Ans：C21 ＝1330 3 (練習1) 在(2x−3y)8的展開式中，x3y5的係數為何？Ans：−1064 (練習2) 在(2x2− 1 x) 8的展開式中，x7的 展開の4つの基本公式 展開についての，基本的な4つの公式を書きます． これらは，左辺を実際に展開すれば導くことができるので，一度は自分で計算してみてください． さて，4つの公式があるとはいえ， ひとまずは一番上の公式 を使えるようになり

簡化多項式方程式兒童數學練習國小國中數學練習題題庫下載列印 教學學習解答

這題 謝謝多項式高一上 Clearnote

泰勒展開式 bee* 1˘ 108 泰勒(1685˘1731，英國人)在1715 年發表泰勒級數，拉格朗日在1797 年提出泰勒多項式的餘 項，泰勒展開式定理則由柯西完成證明。麥克勞林台北市陽明高中數學科 二項分配機率圖 只要輸入試驗的次數（或投擲次數）n，與成功的機率（或正面機率）p，就會畫出對應的「二項分配機率圖」： 張貼者： 10年11月12日 上午1219 pegasus@ymshtpedutw(e) 由多項式的係數決定多項式全體所成的集合： Zx表由全體整係數多項式所成的集合 Qx表由全體有理係數多項式所成的集合 Rx表由全體實係數多項式所成的集合 本單元中，若沒有指定多項式的係數所在的數系，則多項式均為實係數多項式 (4)多項式的相等：

2 1熱身q7 展開多項式 中二數學 Youtube

特征多项式展开公式图片大全 特征多项式展开公式图片在线观看 梨子网

 多項式の基本6｜3次以上の展開と因数分解の公式の総まとめ 前々回の記事で説明したように，たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は，いったん解を求めることによって因数分解できるのでした． では，3次式では因数分解2多項式相等： 設 為兩多項式 若(1)次數相同。 (2)各項係數對應相等，則稱二多項式相等，記做。 3恆等定理 (1)設為一個次多項式，若至少存在 個相異的實數x，使得。則 (表一定值)。 (2)設均為次多項式，若至少存在 個 相異的實數x，使得，則 。概要 主要介绍了 特征多项式 、代数重数、几何重数以及重要 的 性质。 一个复方阵有多少个 特征 值？ 首先要做 的 当然是给出定义啦！ 接下来给出一个结论 ： 证明 ： 我们分三步加以说明， 由 tI−A t I − A 行列式 的 计算 展开 表达式知，只有全取对角

二项式定理 赋值法 普遍适用于恒等式 是一种重要的方法

泰勒公式的麦克劳林展开式 图片信息欣赏 图客 Tukexw Com

式の展開の電卓 展開する式を電卓に入力し「展開」ボタンを押してください。 やり直す場合は「クリア」ボタンを押すと電卓に入力された式が削除されます。 分数の入力に対応しました。 （67追記）X 6 E ® E 1 n!01 正方體的摺紙圖樣 是次課件設計讓學生透過轉動不同的摺紙圖樣中部份面的方向，觀察圖樣摺起時的成果，從而加強學生的立體空間感。 (課件由柯志明先生提供)

资讯 报告 一元 二元泰勒展开 图解高等数学系列03

三项式展开 万图壁纸网

Fzero 指令可用於一般函數的求根，但它一次只能找到一個根，所用的方法是牛頓法。roots 指令只能用於多項式的求根，它能一次找到全部的根，所用的方法是先將多項式表示成「伴隨矩陣」（Companion Matrix），再用解特徵值的方法來求根。 前回からの続き。 マクローリン展開ではないが、最後に三角関数\(cot x\)と双曲線関数\(\coth x\)の多項式展開を扱って1変数関数編を締めたいと思う。三角関数\(\cot x\)の多項式展開 まず前提として、\(\cot x=上式就是「多項式定理」(Multinomial Theorem)。請注意在上式中Σ的右下角不是一個「不等式」，而是一個限制條件，因為對於「多項式定理」而言，難以用上、下限的方式表達其展開式包含哪些項。 例題3：求(a 1 a 2 a 3 a 4) 3 中a 1 2 a 3 的系數。

微積分 泰勒展開式 泰勒展開式例題

特徵多項式 中文数学wiki Fandom

解方程式 求一元一次方程式、二元一次聯立方程式、一元二次方程式、一元三次方程式的解。 求解變數 x y 方程式1 方程式2 計算 清除 錯誤註 若果想計算較低次的多項式的乘積，只要輸入0作為高次的係數即可。 例題 展開且化簡 (3x 2 2x 1)(x 2 2 x 3)。 第一個程式按法 按 Prog 1 再按 3 EXE 2 EXE 1 EXE 1 EXE 2 EXE 3 EXE (顯示x 4 的係數為 3) EXE (顯示x 3 的係數為 4) EXE (顯示x 2 的係數為 6)テイラー多項式・マクローリン多項式 関数 \(f(x)\) の1次近似式を作るためには，導関数 \(f'(x)\) が存在しなければなりません。 さらに，2次近似式を作るためには，2次導関数 \(f''(x)\) が存在しなければなりません。 それでは，関数 \(f(x)\) が3階，4階と微分可能であれば， \(f(x)\) を3次や4次の

二项式定理 维基百科 自由的百科全书

高等数学系列 指数函数的泰勒展开的多项式的根 哔哩哔哩 つロ干杯 Bilibili

关于多项式展开项数问题之经验分享

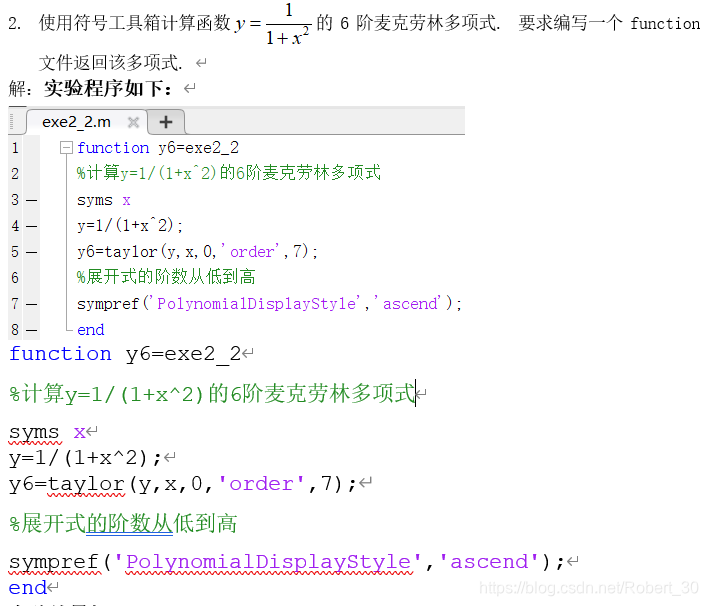
Matlab使用符号工具箱计算函数的5阶麦克劳林多项式的四种方法 附指定阶数 指定点的泰勒展开 Robert 30的博客 程序员资料

二项式系数 快懂百科

泰勒级数 维基百科 自由的百科全书

18年高考二项式定理十大典型问题及例题下载 Word模板 爱问共享资料

复变函数里把函数展开成z的幂级数 两个幂级数相乘怎么解 两个幂级数相乘公式 将函数展开成z的幂级数

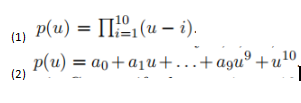
请问如何表示一个多项式并展开 Julia入门 Julia中文社区

高等數學 10 泰勒展開式 第三章微分中值定理 每日頭條

高等數學 11 泰勒公式求極限 第三章微分中值定理 每日頭條

X 1 N展开式 万图壁纸网

多项式定理 万图壁纸网

多项式定理二项式定理升级版 哔哩哔哩 Bilibili

Cf 934d 数学推导多项式展开 Linfanty的博客 Csdn博客

多项式函数在某一点处的泰勒展开 叶卢庆 博客园

二项式定理 维基百科 自由的百科全书

特征多项式展开公式 二十世纪最伟大的十大经典算法 学习岛

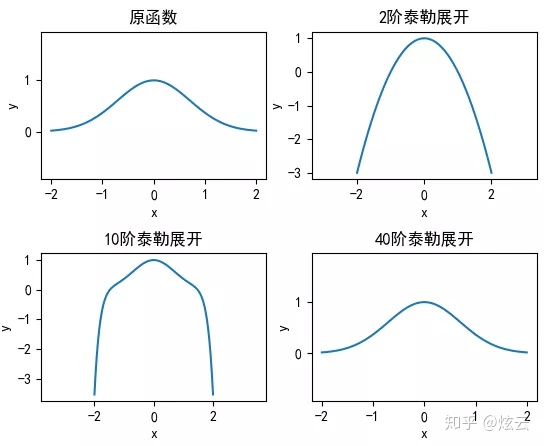
多元函数泰勒级数展开 多项式函数能够拟合非线性问题原理 Weixin 的博客 程序员宅基地 程序员宅基地

泰勒 Taylor 展开式 Ma123rui的博客 Csdn博客 Taylor展开式

头条问答 高中数学泰勒展开式如何应用 梅坞茶香的回答 0赞

多元函数的泰勒展开式 Wx60bf0f6c的技术博客 51cto博客

乗法公式 多項式の展開公式 の覚え方と使い方 数学fun

乘法公式 搜狗百科

多项式展开 N次多项式展开公式 三人行教育网 Www 3rxing Org

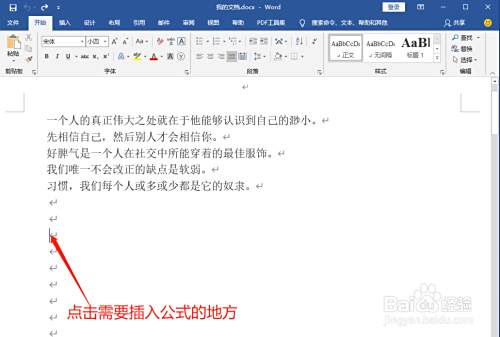
Word如何快速打出多项式展开公式 百度经验

其实可以这样因式分解和多项式展开 每日头条

高考二项式定理十大典型问题及例题 淘文库

关于泰勒展开式的深刻理解 Pursue My Life的博客 Csdn博客

1

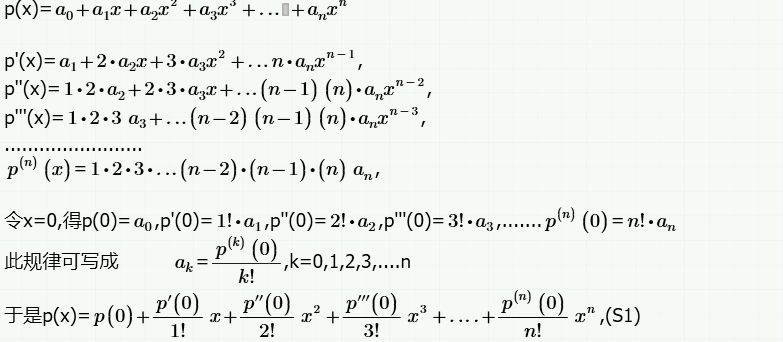
泰勒公式推导及多元泰勒展开式 Linux Bin的博客 Csdn博客 多元泰勒展开式公式

Matlab中的多项式展开 简书

泰勒展開 級數發散能怎麼樣 Getit01

3

多项式乘以多项式练习题 Doc 文档分享网

多項式の展開公式の説明 おかわりドリル

泰勒公式推导及多元泰勒展开式 程序员大本营

泰勒多項式 用多項式函式區域性近似逼近其它複雜的函式 Itw01

N次二项式展开公式 搜狗搜索

二項式定理應用補教教學 二項式定理 係數和的應用 Tbtky

二項式 二項式是只有兩項的多項式 即兩個單項式的和 是僅次於單項式的最簡單多項式 華人百科

A加b的四次方展开式 西瓜视频搜索

函数展开成幂级数及其应用 Jason S Blog

3 1 熱身q9 展開多項式 中二數學 Youtube

泰勒公式推导及多元泰勒展开式 Linux Bin的博客 Csdn博客 多元泰勒展开式公式

多项式展开 Explore Facebook

高中数学37个解题大招之三 二项式定理常考9大题型总结 超实用 教育资讯 游戏新闻

怎样将部分分式展开 百度经验

Math 泰勒展開式taylor S Expanasion Terry部落格

按 X 4 的幂展开多项式f X X 4 5x 3 X 2 3x 4 数学竞赛平台 数学帮 Math110

68 分母为多项式的幂的分数函数的无穷级数展开 简书

1 3 二项式定理 题后感悟 方法二较为简单 在展开二项式之前根据二项式的结构特征进行适当变形 可使展开多项式的过程简化 记准 记熟二项式

泰勒级数展开函数展开成幂级数有什么用这不是和泰勒公式差不多吗 比乐族

Q Sincostancotseccsc Asinacosatanacotasecacsc Explogsqrtlog 2log 10 Absconjrealimag Rankdetinveig

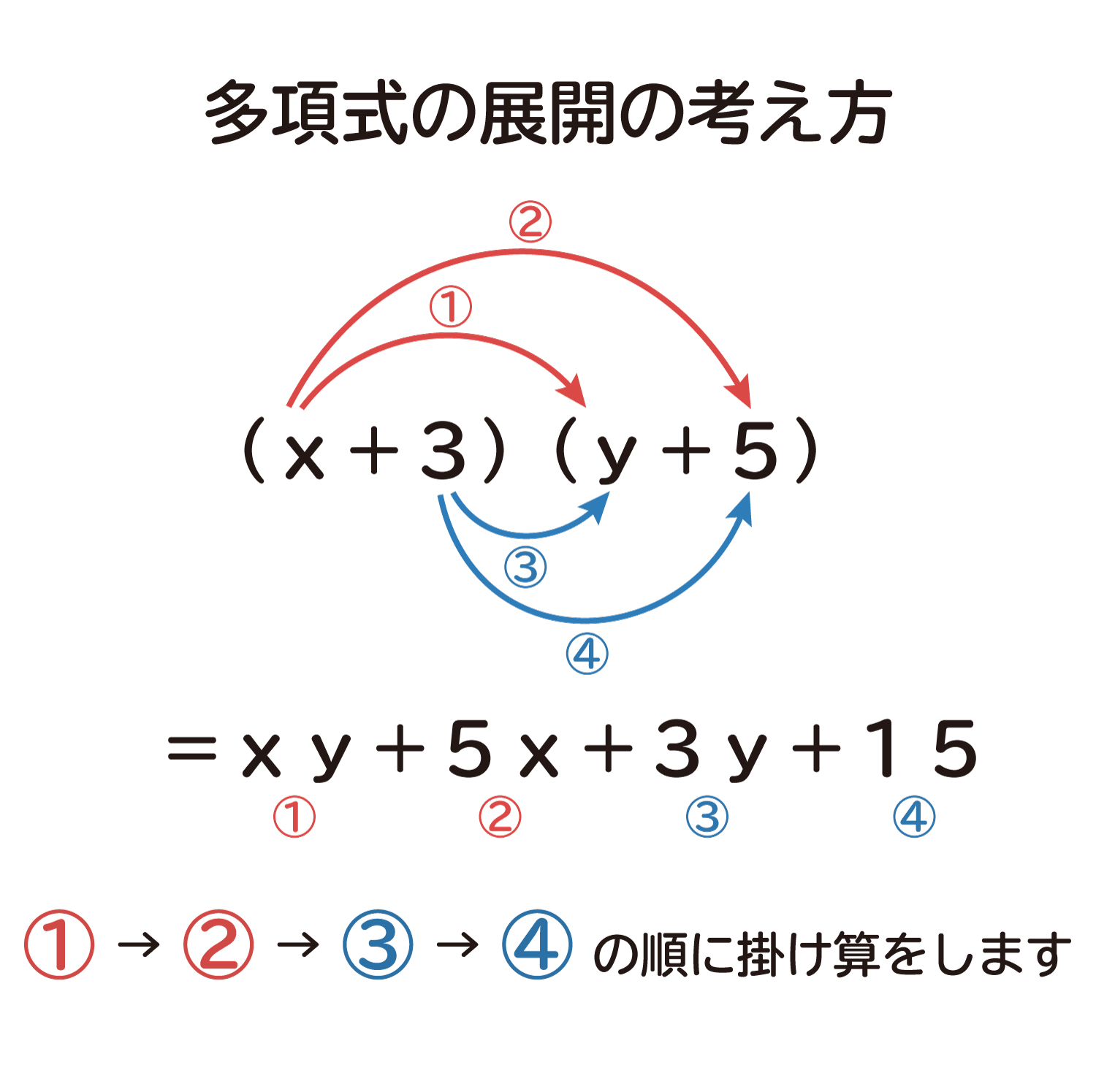
多項式同士の掛け算の展開の考え方 おかわりドリル

多元函数的泰勒 Taylor 展开式 Jensen Lee的博客 程序员资料 多元函数的泰勒公式 程序员资料

2 4 Ex6 多項式展開求係數 Youtube

多项式展开式系数公式 扒拉扒拉

数值积分 泰勒 Taylor 公式求积分 数值分析与有限元编程 微信公众号文章阅读 Wemp

函数的泰勒展开式 程序员大本营

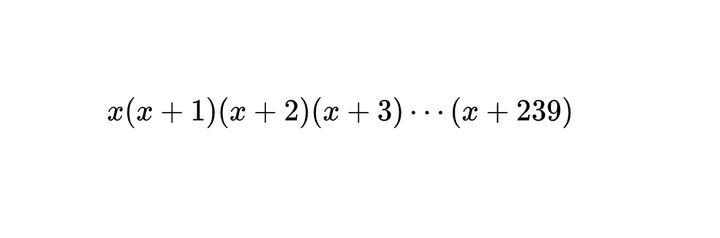
多项式展开里面有多少项是3的倍数 知乎

特征多项式展开公式矩阵的特征多项式的展开式是什么形式 是如何推出的 需要具体的过 全球牛商网

9 5多项式的因式分解 西瓜视频搜索

多项式的n次方展开项数 多项式n次方展开式 光辉网络

1

题目集合母函数 生成函数 普通型型母函数指数型母函数 涉及知识点背包多项式乘法排列组合泰勒展开 Andromeda Galaxy 博客园

關於泰勒展開 台部落

多项式函数在某一点处的泰勒展开 叶卢庆 博客园

高中数学中的泰勒公式 函数

4 5 いまさらきけない多項式 展開の練習 理一の数学事始め Note

3 13多項式乘除法

多項式展開公式多項式的相乘公式 Xxjexy

二項式定理原理及其範例 Youtube

高考专题讲解之二项式定理下载 Word模板 爱问共享资料

泰勒展開式e Taylor S Fvilb

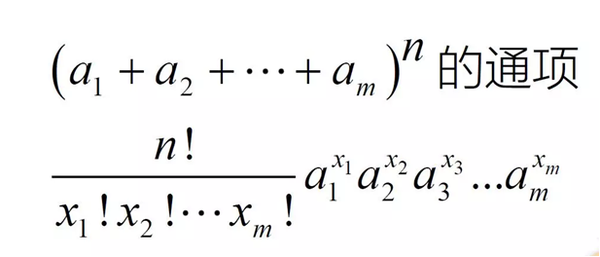
什么 多项式定理都不会 从此三项式秒杀 知乎

多项式展开 Explore Facebook

多项式展开项系数公式 西瓜视频搜索

幂级数连分式展开 多项式分式展开为幂级数的问题 三人行教育网 Www 3rxing Org

利用泰勒公式求极限 函数需要展开到第几阶 知乎

多项式二次方程的因式分解数学多项式展开 数学png图片素材免费下载 图片编号 Png素材网

因式分解

22mba考研 管理类联考每日一练 数学 多项式展开式中系数 Mba工商管理硕士 上海众凯考研辅导

76 一般的常数项为1的多项式幂的无穷级数展开 简书

数学笔记31 幂级数和泰勒级数 Wx60bddca97d334的技术博客 51cto博客

函数的幂级数展开 菜瓜变菜鸟 程序员宝宝 程序员宝宝

多项式展开公式证明 N次多项式展开公式 三人行教育网 Www 3rxing Org

常用泰勒公式及展开小专题 腾讯新闻

多項式展開 Ruralred

数学实验4 符号变量与符号表达式微积分基本运算级数求和与泰勒展开式常微分方程符号解符号变量的定义